Adaptation to the Range in $K$-Armed Bandits

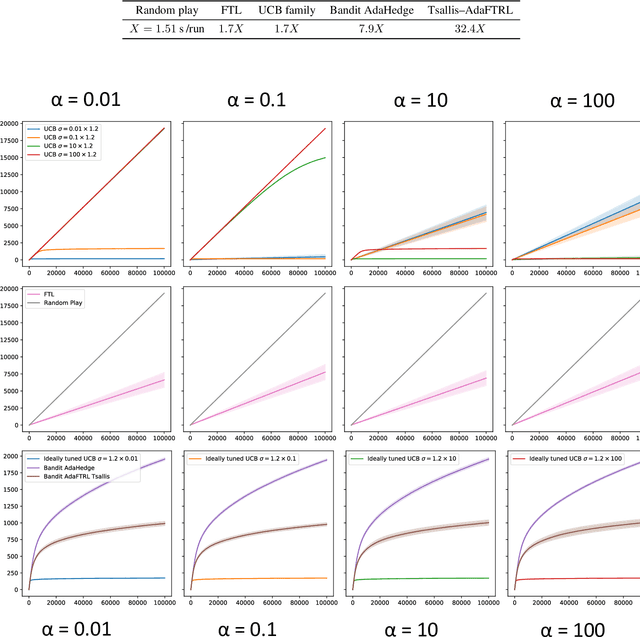
We consider stochastic bandit problems with $K$ arms, each associated with a bounded distribution supported on the range $[m,M]$. We do not assume that the range $[m,M]$ is known and show that there is a cost for learning this range. Indeed, a new trade-off between distribution-dependent and distribution-free regret bounds arises, which, for instance, prevents from simultaneously achieving the typical $\ln T$ and $\sqrt{T}$ bounds. For instance, a $\sqrt{T}$ distribution-free regret bound may only be achieved if the distribution-dependent regret bounds are at least of order $\sqrt{T}$. We exhibit a strategy achieving the rates for regret indicated by the new trade-off.