Demographic Parity Tails for Regression

Demographic parity (DP) is a widely studied fairness criterion in regression, enforcing independence between the predictions and sensitive attributes. However, constraining the entire distribution can degrade predictive accuracy and may be unnecessary for many applications, where fairness concerns are localized to specific regions of the distribution. To overcome this issue, we propose a new framework for regression under DP that focuses on the tails of target distribution across sensitive groups. Our methodology builds on optimal transport theory. By enforcing fairness constraints only over targeted regions of the distribution, our approach enables more nuanced and context-sensitive interventions. Leveraging recent advances, we develop an interpretable and flexible algorithm that leverages the geometric structure of optimal transport. We provide theoretical guarantees, including risk bounds and fairness properties, and validate the method through experiments in regression settings.

Fair regression under localized demographic parity constraints

Demographic parity (DP) is a widely used group fairness criterion requiring predictive distributions to be invariant across sensitive groups. While natural in classification, full distributional DP is often overly restrictive in regression and can lead to substantial accuracy loss. We propose a relaxation of DP tailored to regression, enforcing parity only at a finite set of quantile levels and/or score thresholds. Concretely, we introduce a novel (${\ell}$, Z)-fair predictor, which imposes groupwise CDF constraints of the form F f |S=s (z m ) = ${\ell}$ m for prescribed pairs (${\ell}$ m , z m ). For this setting, we derive closed-form characterizations of the optimal fair discretized predictor via a Lagrangian dual formulation and quantify the discretization cost, showing that the risk gap to the continuous optimum vanishes as the grid is refined. We further develop a model-agnostic post-processing algorithm based on two samples (labeled for learning a base regressor and unlabeled for calibration), and establish finite-sample guarantees on constraint violation and excess penalized risk. In addition, we introduce two alternative frameworks where we match group and marginal CDF values at selected score thresholds. In both settings, we provide closed-form solutions for the optimal fair discretized predictor. Experiments on synthetic and real datasets illustrate an interpretable fairness-accuracy trade-off, enabling targeted corrections at decision-relevant quantiles or thresholds while preserving predictive performance.

Set to Be Fair: Demographic Parity Constraints for Set-Valued Classification

Set-valued classification is used in multiclass settings where confusion between classes can occur and lead to misleading predictions. However, its application may amplify discriminatory bias motivating the development of set-valued approaches under fairness constraints. In this paper, we address the problem of set-valued classification under demographic parity and expected size constraints. We propose two complementary strategies: an oracle-based method that minimizes classification risk while satisfying both constraints, and a computationally efficient proxy that prioritizes constraint satisfaction. For both strategies, we derive closed-form expressions for the (optimal) fair set-valued classifiers and use these to build plug-in, data-driven procedures for empirical predictions. We establish distribution-free convergence rates for violations of the size and fairness constraints for both methods, and under mild assumptions we also provide excess-risk bounds for the oracle-based approach. Empirical results demonstrate the effectiveness of both strategies and highlight the efficiency of our proxy method.

Empirical risk minimization algorithm for multiclass classification of S.D.E. paths

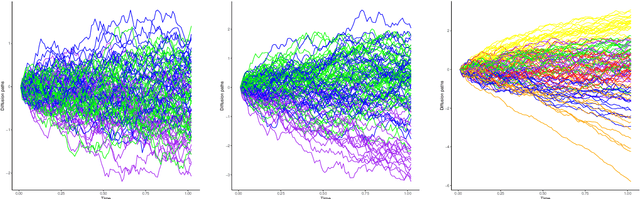
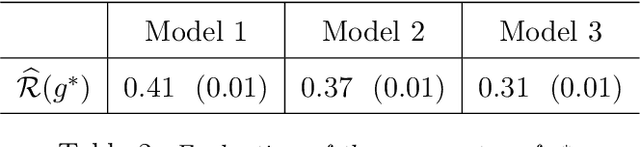
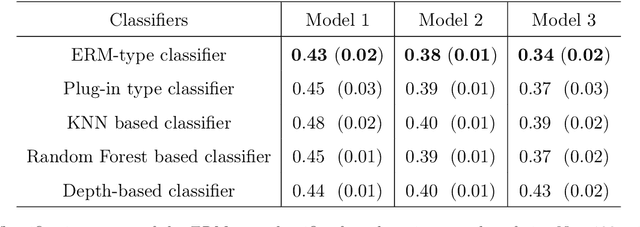
We address the multiclass classification problem for stochastic diffusion paths, assuming that the classes are distinguished by their drift functions, while the diffusion coefficient remains common across all classes. In this setting, we propose a classification algorithm that relies on the minimization of the L 2 risk. We establish rates of convergence for the resulting predictor. Notably, we introduce a margin assumption under which we show that our procedure can achieve fast rates of convergence. Finally, a simulation study highlights the numerical performance of our classification algorithm.

Nonparametric plug-in classifier for multiclass classification of S.D.E. paths

We study the multiclass classification problem where the features come from the mixture of time-homogeneous diffusions. Specifically, the classes are discriminated by their drift functions while the diffusion coefficient is common to all classes and unknown. In this framework, we build a plug-in classifier which relies on nonparametric estimators of the drift and diffusion functions. We first establish the consistency of our classification procedure under mild assumptions and then provide rates of cnvergence under different set of assumptions. Finally, a numerical study supports our theoretical findings.

Set-valued classification -- overview via a unified framework

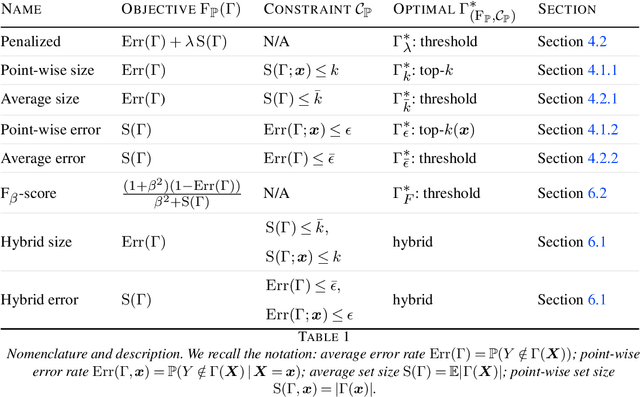
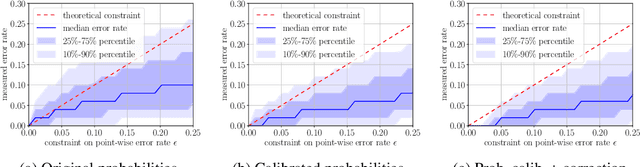
Multi-class classification problem is among the most popular and well-studied statistical frameworks. Modern multi-class datasets can be extremely ambiguous and single-output predictions fail to deliver satisfactory performance. By allowing predictors to predict a set of label candidates, set-valued classification offers a natural way to deal with this ambiguity. Several formulations of set-valued classification are available in the literature and each of them leads to different prediction strategies. The present survey aims to review popular formulations using a unified statistical framework. The proposed framework encompasses previously considered and leads to new formulations as well as it allows to understand underlying trade-offs of each formulation. We provide infinite sample optimal set-valued classification strategies and review a general plug-in principle to construct data-driven algorithms. The exposition is supported by examples and pointers to both theoretical and practical contributions. Finally, we provide experiments on real-world datasets comparing these approaches in practice and providing general practical guidelines.

Regression with reject option and application to kNN

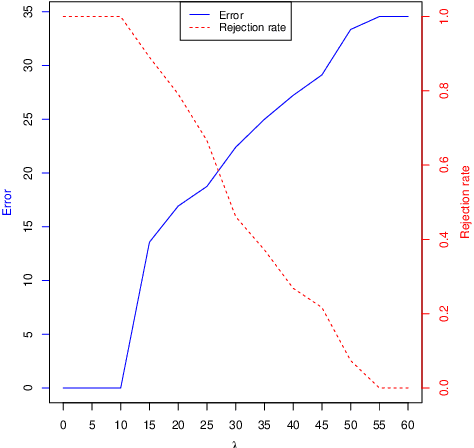
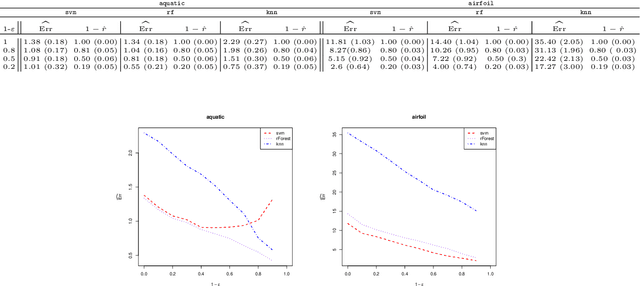
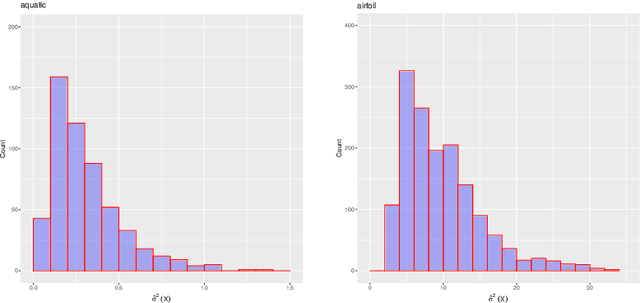
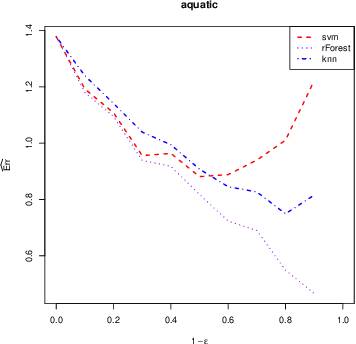
We investigate the problem of regression where one is allowed to abstain from predicting. We refer to this framework as regression with reject option as an extension of classification with reject option. In this context, we focus on the case where the rejection rate is fixed and derive the optimal rule which relies on thresholding the conditional variance function. We provide a semi-supervised estimation procedure of the optimal rule involving two datasets: a first labeled dataset is used to estimate both regression function and conditional variance function while a second unlabeled dataset is exploited to calibrate the desired rejection rate. The resulting predictor with reject option is shown to be almost as good as the optimal predictor with reject option both in terms of risk and rejection rate. We additionally apply our methodology with kNN algorithm and establish rates of convergence for the resulting kNN predictor under mild conditions. Finally, a numerical study is performed to illustrate the benefit of using the proposed procedure.

Fair Regression with Wasserstein Barycenters

We study the problem of learning a real-valued function that satisfies the Demographic Parity constraint. It demands the distribution of the predicted output to be independent of the sensitive attribute. We consider the case that the sensitive attribute is available for prediction. We establish a connection between fair regression and optimal transport theory, based on which we derive a close form expression for the optimal fair predictor. Specifically, we show that the distribution of this optimum is the Wasserstein barycenter of the distributions induced by the standard regression function on the sensitive groups. This result offers an intuitive interpretation of the optimal fair prediction and suggests a simple post-processing algorithm to achieve fairness. We establish risk and distribution-free fairness guarantees for this procedure. Numerical experiments indicate that our method is very effective in learning fair models, with a relative increase in error rate that is inferior to the relative gain in fairness.

Leveraging Labeled and Unlabeled Data for Consistent Fair Binary Classification

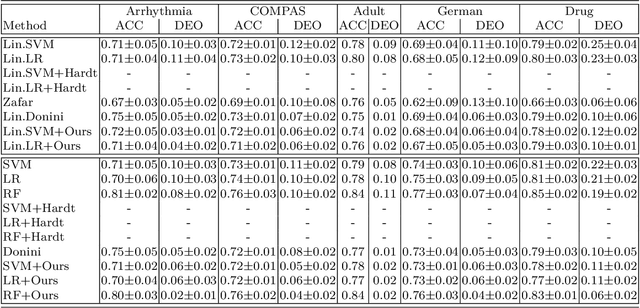
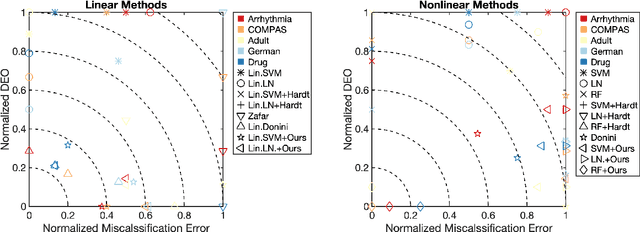
We study the problem of fair binary classification using the notion of Equal Opportunity. It requires the true positive rate to distribute equally across the sensitive groups. Within this setting we show that the fair optimal classifier is obtained by recalibrating the Bayes classifier by a group-dependent threshold. We provide a constructive expression for the threshold. This result motivates us to devise a plug-in classification procedure based on both unlabeled and labeled datasets. While the latter is used to learn the output conditional probability, the former is used for calibration. The overall procedure can be computed in polynomial time and it is shown to be statistically consistent both in terms of classification error and fairness measure. Finally, we present numerical experiments which indicate that our method is often superior or competitive with the state-of-the-art methods on benchmark datasets.

On the benefits of output sparsity for multi-label classification

The multi-label classification framework, where each observation can be associated with a set of labels, has generated a tremendous amount of attention over recent years. The modern multi-label problems are typically large-scale in terms of number of observations, features and labels, and the amount of labels can even be comparable with the amount of observations. In this context, different remedies have been proposed to overcome the curse of dimensionality. In this work, we aim at exploiting the output sparsity by introducing a new loss, called the sparse weighted Hamming loss. This proposed loss can be seen as a weighted version of classical ones, where active and inactive labels are weighted separately. Leveraging the influence of sparsity in the loss function, we provide improved generalization bounds for the empirical risk minimizer, a suitable property for large-scale problems. For this new loss, we derive rates of convergence linear in the underlying output-sparsity rather than linear in the number of labels. In practice, minimizing the associated risk can be performed efficiently by using convex surrogates and modern convex optimization algorithms. We provide experiments on various real-world datasets demonstrating the pertinence of our approach when compared to non-weighted techniques.