Variance function estimation in regression model via aggregation procedures

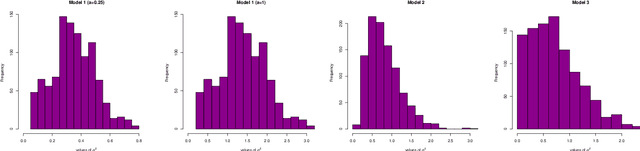
In the regression problem, we consider the problem of estimating the variance function by the means of aggregation methods. We focus on two particular aggregation setting: Model Selection aggregation (MS) and Convex aggregation (C) where the goal is to select the best candidate and to build the best convex combination of candidates respectively among a collection of candidates. In both cases, the construction of the estimator relies on a two-step procedure and requires two independent samples. The first step exploits the first sample to build the candidate estimators for the variance function by the residual-based method and then the second dataset is used to perform the aggregation step. We show the consistency of the proposed method with respect to the L 2error both for MS and C aggregations. We evaluate the performance of these two methods in the heteroscedastic model and illustrate their interest in the regression problem with reject option.

Regression with reject option and application to kNN

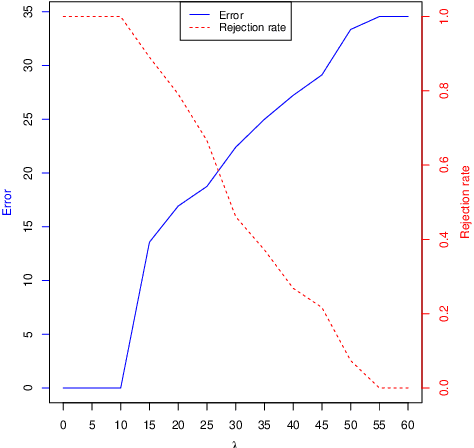
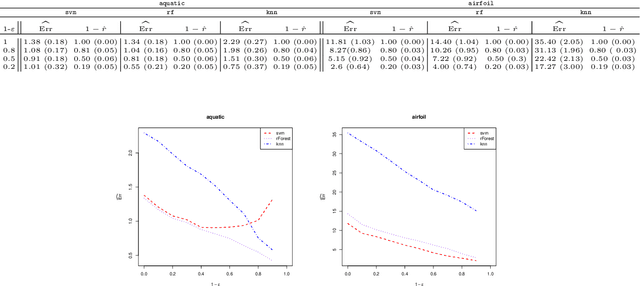
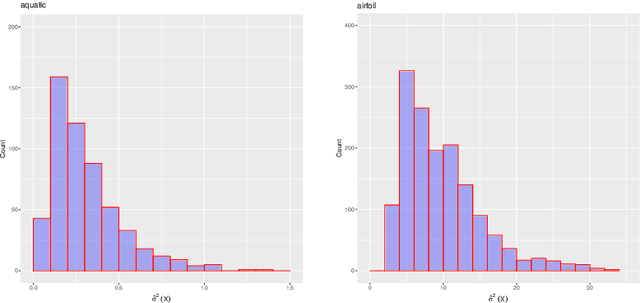
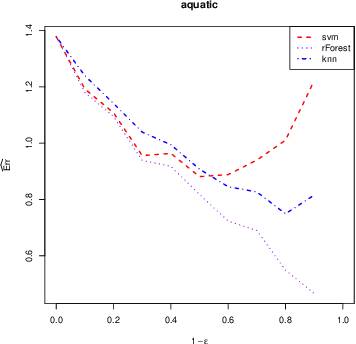
We investigate the problem of regression where one is allowed to abstain from predicting. We refer to this framework as regression with reject option as an extension of classification with reject option. In this context, we focus on the case where the rejection rate is fixed and derive the optimal rule which relies on thresholding the conditional variance function. We provide a semi-supervised estimation procedure of the optimal rule involving two datasets: a first labeled dataset is used to estimate both regression function and conditional variance function while a second unlabeled dataset is exploited to calibrate the desired rejection rate. The resulting predictor with reject option is shown to be almost as good as the optimal predictor with reject option both in terms of risk and rejection rate. We additionally apply our methodology with kNN algorithm and establish rates of convergence for the resulting kNN predictor under mild conditions. Finally, a numerical study is performed to illustrate the benefit of using the proposed procedure.