Training-Free Constrained Generation With Stable Diffusion Models

Stable diffusion models represent the state-of-the-art in data synthesis across diverse domains and hold transformative potential for applications in science and engineering, e.g., by facilitating the discovery of novel solutions and simulating systems that are computationally intractable to model explicitly. However, their current utility in these fields is severely limited by an inability to enforce strict adherence to physical laws and domain-specific constraints. Without this grounding, the deployment of such models in critical applications, ranging from material science to safety-critical systems, remains impractical. This paper addresses this fundamental limitation by proposing a novel approach to integrate stable diffusion models with constrained optimization frameworks, enabling them to generate outputs that satisfy stringent physical and functional requirements. We demonstrate the effectiveness of this approach through material science experiments requiring adherence to precise morphometric properties, inverse design problems involving the generation of stress-strain responses using video generation with a simulator in the loop, and safety settings where outputs must avoid copyright infringement.

Analyzing and Enhancing the Backward-Pass Convergence of Unrolled Optimization

The integration of constrained optimization models as components in deep networks has led to promising advances on many specialized learning tasks. A central challenge in this setting is backpropagation through the solution of an optimization problem, which often lacks a closed form. One typical strategy is algorithm unrolling, which relies on automatic differentiation through the entire chain of operations executed by an iterative optimization solver. This paper provides theoretical insights into the backward pass of unrolled optimization, showing that it is asymptotically equivalent to the solution of a linear system by a particular iterative method. Several practical pitfalls of unrolling are demonstrated in light of these insights, and a system called Folded Optimization is proposed to construct more efficient backpropagation rules from unrolled solver implementations. Experiments over various end-to-end optimization and learning tasks demonstrate the advantages of this system both computationally, and in terms of flexibility over various optimization problem forms.

Predict-Then-Optimize by Proxy: Learning Joint Models of Prediction and Optimization

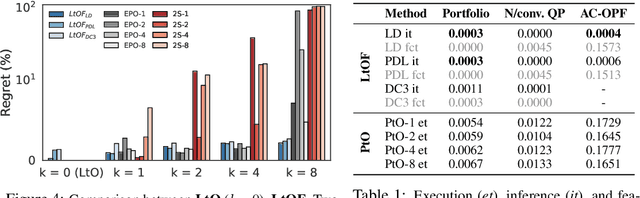
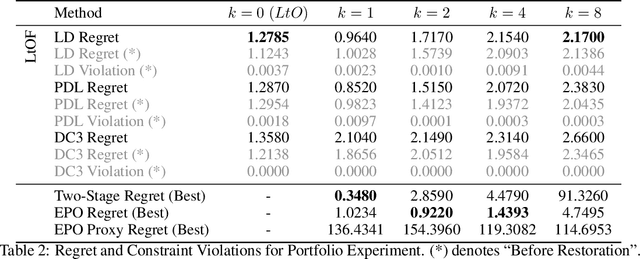
Many real-world decision processes are modeled by optimization problems whose defining parameters are unknown and must be inferred from observable data. The Predict-Then-Optimize framework uses machine learning models to predict unknown parameters of an optimization problem from features before solving. Recent works show that decision quality can be improved in this setting by solving and differentiating the optimization problem in the training loop, enabling end-to-end training with loss functions defined directly on the resulting decisions. However, this approach can be inefficient and requires handcrafted, problem-specific rules for backpropagation through the optimization step. This paper proposes an alternative method, in which optimal solutions are learned directly from the observable features by predictive models. The approach is generic, and based on an adaptation of the Learning-to-Optimize paradigm, from which a rich variety of existing techniques can be employed. Experimental evaluations show the ability of several Learning-to-Optimize methods to provide efficient, accurate, and flexible solutions to an array of challenging Predict-Then-Optimize problems.