On the Sample Complexity of a Policy Gradient Algorithm with Occupancy Approximation for General Utility Reinforcement Learning
Paper and Code
Oct 05, 2024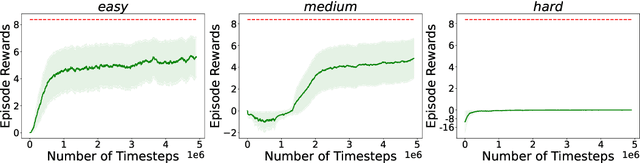
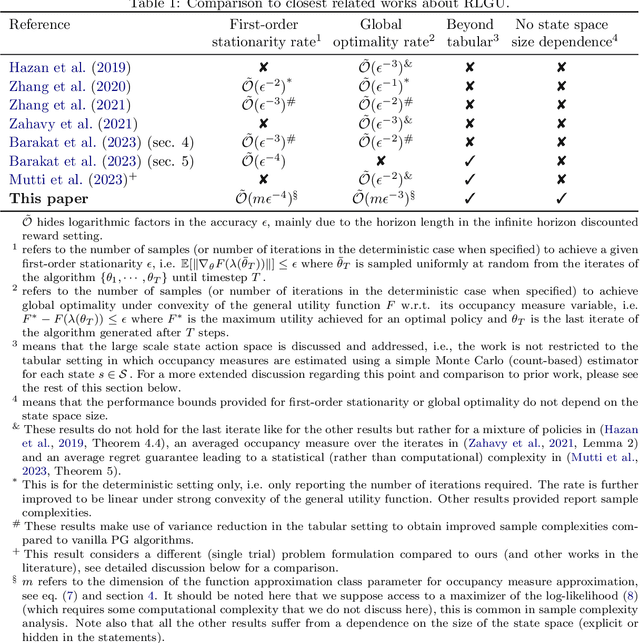
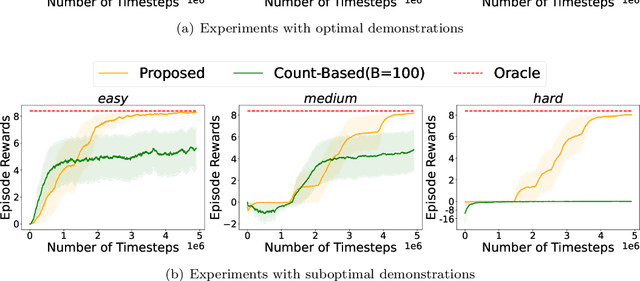
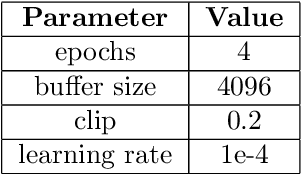
Reinforcement learning with general utilities has recently gained attention thanks to its ability to unify several problems, including imitation learning, pure exploration, and safe RL. However, prior work for solving this general problem in a unified way has mainly focused on the tabular setting. This is restrictive when considering larger state-action spaces because of the need to estimate occupancy measures during policy optimization. In this work, we address this issue and propose to approximate occupancy measures within a function approximation class using maximum likelihood estimation (MLE). We propose a simple policy gradient algorithm (PG-OMA) where an actor updates the policy parameters to maximize the general utility objective whereas a critic approximates the occupancy measure using MLE. We provide a sample complexity analysis of PG-OMA showing that our occupancy measure estimation error only scales with the dimension of our function approximation class rather than the size of the state action space. Under suitable assumptions, we establish first order stationarity and global optimality performance bounds for the proposed PG-OMA algorithm for nonconcave and concave general utilities respectively. We complement our methodological and theoretical findings with promising empirical results showing the scalability potential of our approach compared to existing tabular count-based approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge