Can SGD Handle Heavy-Tailed Noise?

Stochastic Gradient Descent (SGD) is a cornerstone of large-scale optimization, yet its theoretical behavior under heavy-tailed noise -- common in modern machine learning and reinforcement learning -- remains poorly understood. In this work, we rigorously investigate whether vanilla SGD, devoid of any adaptive modifications, can provably succeed under such adverse stochastic conditions. Assuming only that stochastic gradients have bounded $p$-th moments for some $p \in (1, 2]$, we establish sharp convergence guarantees for (projected) SGD across convex, strongly convex, and non-convex problem classes. In particular, we show that SGD achieves minimax optimal sample complexity under minimal assumptions in the convex and strongly convex regimes: $\mathcal{O}(\varepsilon^{-\frac{p}{p-1}})$ and $\mathcal{O}(\varepsilon^{-\frac{p}{2(p-1)}})$, respectively. For non-convex objectives under H\"older smoothness, we prove convergence to a stationary point with rate $\mathcal{O}(\varepsilon^{-\frac{2p}{p-1}})$, and complement this with a matching lower bound specific to SGD with arbitrary polynomial step-size schedules. Finally, we consider non-convex Mini-batch SGD under standard smoothness and bounded central moment assumptions, and show that it also achieves a comparable $\mathcal{O}(\varepsilon^{-\frac{2p}{p-1}})$ sample complexity with a potential improvement in the smoothness constant. These results challenge the prevailing view that heavy-tailed noise renders SGD ineffective, and establish vanilla SGD as a robust and theoretically principled baseline -- even in regimes where the variance is unbounded.

From Gradient Clipping to Normalization for Heavy Tailed SGD

Recent empirical evidence indicates that many machine learning applications involve heavy-tailed gradient noise, which challenges the standard assumptions of bounded variance in stochastic optimization. Gradient clipping has emerged as a popular tool to handle this heavy-tailed noise, as it achieves good performance in this setting both theoretically and practically. However, our current theoretical understanding of non-convex gradient clipping has three main shortcomings. First, the theory hinges on large, increasing clipping thresholds, which are in stark contrast to the small constant clipping thresholds employed in practice. Second, clipping thresholds require knowledge of problem-dependent parameters to guarantee convergence. Lastly, even with this knowledge, current sampling complexity upper bounds for the method are sub-optimal in nearly all parameters. To address these issues, we study convergence of Normalized SGD (NSGD). First, we establish a parameter-free sample complexity for NSGD of $\mathcal{O}\left(\varepsilon^{-\frac{2p}{p-1}}\right)$ to find an $\varepsilon$-stationary point. Furthermore, we prove tightness of this result, by providing a matching algorithm-specific lower bound. In the setting where all problem parameters are known, we show this complexity is improved to $\mathcal{O}\left(\varepsilon^{-\frac{3p-2}{p-1}}\right)$, matching the previously known lower bound for all first-order methods in all problem dependent parameters. Finally, we establish high-probability convergence of NSGD with a mild logarithmic dependence on the failure probability. Our work complements the studies of gradient clipping under heavy tailed noise improving the sample complexities of existing algorithms and offering an alternative mechanism to achieve high probability convergence.

Parameter-Agnostic Optimization under Relaxed Smoothness

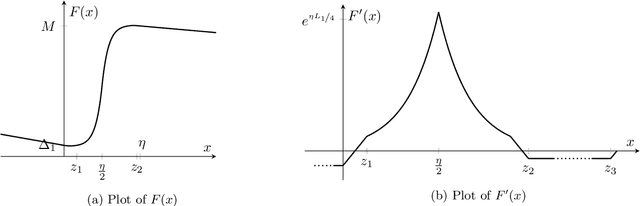
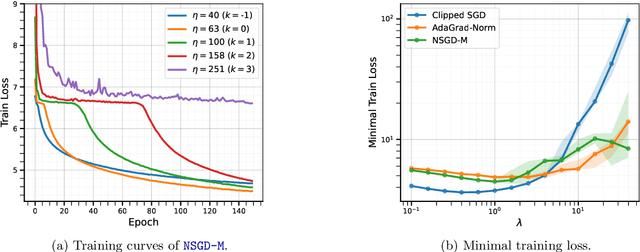
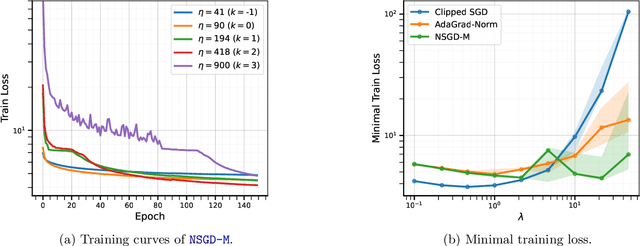
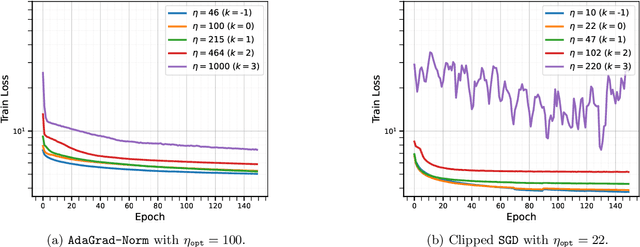
Tuning hyperparameters, such as the stepsize, presents a major challenge of training machine learning models. To address this challenge, numerous adaptive optimization algorithms have been developed that achieve near-optimal complexities, even when stepsizes are independent of problem-specific parameters, provided that the loss function is $L$-smooth. However, as the assumption is relaxed to the more realistic $(L_0, L_1)$-smoothness, all existing convergence results still necessitate tuning of the stepsize. In this study, we demonstrate that Normalized Stochastic Gradient Descent with Momentum (NSGD-M) can achieve a (nearly) rate-optimal complexity without prior knowledge of any problem parameter, though this comes at the cost of introducing an exponential term dependent on $L_1$ in the complexity. We further establish that this exponential term is inevitable to such schemes by introducing a theoretical framework of lower bounds tailored explicitly for parameter-agnostic algorithms. Interestingly, in deterministic settings, the exponential factor can be neutralized by employing Gradient Descent with a Backtracking Line Search. To the best of our knowledge, these findings represent the first parameter-agnostic convergence results under the generalized smoothness condition. Our empirical experiments further confirm our theoretical insights.