Gradient Descent as a Perceptron Algorithm: Understanding Dynamics and Implicit Acceleration

Even for the gradient descent (GD) method applied to neural network training, understanding its optimization dynamics, including convergence rate, iterate trajectories, function value oscillations, and especially its implicit acceleration, remains a challenging problem. We analyze nonlinear models with the logistic loss and show that the steps of GD reduce to those of generalized perceptron algorithms (Rosenblatt, 1958), providing a new perspective on the dynamics. This reduction yields significantly simpler algorithmic steps, which we analyze using classical linear algebra tools. Using these tools, we demonstrate on a minimalistic example that the nonlinearity in a two-layer model can provably yield a faster iteration complexity $\tilde{O}(\sqrt{d})$ compared to $Ω(d)$ achieved by linear models, where $d$ is the number of features. This helps explain the optimization dynamics and the implicit acceleration phenomenon observed in neural networks. The theoretical results are supported by extensive numerical experiments. We believe that this alternative view will further advance research on the optimization of neural networks.

Near-Optimal Convergence of Accelerated Gradient Methods under Generalized and $(L_0, L_1)$-Smoothness

We study first-order methods for convex optimization problems with functions $f$ satisfying the recently proposed $\ell$-smoothness condition $||\nabla^{2}f(x)|| \le \ell\left(||\nabla f(x)||\right),$ which generalizes the $L$-smoothness and $(L_{0},L_{1})$-smoothness. While accelerated gradient descent AGD is known to reach the optimal complexity $O(\sqrt{L} R / \sqrt{\varepsilon})$ under $L$-smoothness, where $\varepsilon$ is an error tolerance and $R$ is the distance between a starting and an optimal point, existing extensions to $\ell$-smoothness either incur extra dependence on the initial gradient, suffer exponential factors in $L_{1} R$, or require costly auxiliary sub-routines, leaving open whether an AGD-type $O(\sqrt{\ell(0)} R / \sqrt{\varepsilon})$ rate is possible for small-$\varepsilon$, even in the $(L_{0},L_{1})$-smoothness case. We resolve this open question. Leveraging a new Lyapunov function and designing new algorithms, we achieve $O(\sqrt{\ell(0)} R / \sqrt{\varepsilon})$ oracle complexity for small-$\varepsilon$ and virtually any $\ell$. For instance, for $(L_{0},L_{1})$-smoothness, our bound $O(\sqrt{L_0} R / \sqrt{\varepsilon})$ is provably optimal in the small-$\varepsilon$ regime and removes all non-constant multiplicative factors present in prior accelerated algorithms.

Birch SGD: A Tree Graph Framework for Local and Asynchronous SGD Methods

We propose a new unifying framework, Birch SGD, for analyzing and designing distributed SGD methods. The central idea is to represent each method as a weighted directed tree, referred to as a computation tree. Leveraging this representation, we introduce a general theoretical result that reduces convergence analysis to studying the geometry of these trees. This perspective yields a purely graph-based interpretation of optimization dynamics, offering a new and intuitive foundation for method development. Using Birch SGD, we design eight new methods and analyze them alongside previously known ones, with at least six of the new methods shown to have optimal computational time complexity. Our research leads to two key insights: (i) all methods share the same "iteration rate" of $O\left(\frac{(R + 1) L \Delta}{\varepsilon} + \frac{\sigma^2 L \Delta}{\varepsilon^2}\right)$, where $R$ the maximum "tree distance" along the main branch of a tree; and (ii) different methods exhibit different trade-offs-for example, some update iterates more frequently, improving practical performance, while others are more communication-efficient or focus on other aspects. Birch SGD serves as a unifying framework for navigating these trade-offs. We believe these results provide a unified foundation for understanding, analyzing, and designing efficient asynchronous and parallel optimization methods.

Ringmaster ASGD: The First Asynchronous SGD with Optimal Time Complexity

Asynchronous Stochastic Gradient Descent (Asynchronous SGD) is a cornerstone method for parallelizing learning in distributed machine learning. However, its performance suffers under arbitrarily heterogeneous computation times across workers, leading to suboptimal time complexity and inefficiency as the number of workers scales. While several Asynchronous SGD variants have been proposed, recent findings by Tyurin & Richt\'arik (NeurIPS 2023) reveal that none achieve optimal time complexity, leaving a significant gap in the literature. In this paper, we propose Ringmaster ASGD, a novel Asynchronous SGD method designed to address these limitations and tame the inherent challenges of Asynchronous SGD. We establish, through rigorous theoretical analysis, that Ringmaster ASGD achieves optimal time complexity under arbitrarily heterogeneous and dynamically fluctuating worker computation times. This makes it the first Asynchronous SGD method to meet the theoretical lower bounds for time complexity in such scenarios.

From Logistic Regression to the Perceptron Algorithm: Exploring Gradient Descent with Large Step Sizes

We focus on the classification problem with a separable dataset, one of the most important and classical problems from machine learning. The standard approach to this task is logistic regression with gradient descent (LR+GD). Recent studies have observed that LR+GD can find a solution with arbitrarily large step sizes, defying conventional optimization theory. Our work investigates this phenomenon and makes three interconnected key observations about LR+GD with large step sizes. First, we find a remarkably simple explanation of why LR+GD with large step sizes solves the classification problem: LR+GD reduces to a batch version of the celebrated perceptron algorithm when the step size $\gamma \to \infty.$ Second, we observe that larger step sizes lead LR+GD to higher logistic losses when it tends to the perceptron algorithm, but larger step sizes also lead to faster convergence to a solution for the classification problem, meaning that logistic loss is an unreliable metric of the proximity to a solution. Surprisingly, high loss values can actually indicate faster convergence. Third, since the convergence rate in terms of loss function values of LR+GD is unreliable, we examine the iteration complexity required by LR+GD with large step sizes to solve the classification problem and prove that this complexity is suboptimal. To address this, we propose a new method, Normalized LR+GD - based on the connection between LR+GD and the perceptron algorithm - with much better theoretical guarantees.

Tighter Performance Theory of FedExProx

We revisit FedExProx - a recently proposed distributed optimization method designed to enhance convergence properties of parallel proximal algorithms via extrapolation. In the process, we uncover a surprising flaw: its known theoretical guarantees on quadratic optimization tasks are no better than those offered by the vanilla Gradient Descent (GD) method. Motivated by this observation, we develop a novel analysis framework, establishing a tighter linear convergence rate for non-strongly convex quadratic problems. By incorporating both computation and communication costs, we demonstrate that FedExProx can indeed provably outperform GD, in stark contrast to the original analysis. Furthermore, we consider partial participation scenarios and analyze two adaptive extrapolation strategies - based on gradient diversity and Polyak stepsizes - again significantly outperforming previous results. Moving beyond quadratics, we extend the applicability of our analysis to general functions satisfying the Polyak-Lojasiewicz condition, outperforming the previous strongly convex analysis while operating under weaker assumptions. Backed by empirical results, our findings point to a new and stronger potential of FedExProx, paving the way for further exploration of the benefits of extrapolation in federated learning.

Freya PAGE: First Optimal Time Complexity for Large-Scale Nonconvex Finite-Sum Optimization with Heterogeneous Asynchronous Computations

In practical distributed systems, workers are typically not homogeneous, and due to differences in hardware configurations and network conditions, can have highly varying processing times. We consider smooth nonconvex finite-sum (empirical risk minimization) problems in this setup and introduce a new parallel method, Freya PAGE, designed to handle arbitrarily heterogeneous and asynchronous computations. By being robust to "stragglers" and adaptively ignoring slow computations, Freya PAGE offers significantly improved time complexity guarantees compared to all previous methods, including Asynchronous SGD, Rennala SGD, SPIDER, and PAGE, while requiring weaker assumptions. The algorithm relies on novel generic stochastic gradient collection strategies with theoretical guarantees that can be of interest on their own, and may be used in the design of future optimization methods. Furthermore, we establish a lower bound for smooth nonconvex finite-sum problems in the asynchronous setup, providing a fundamental time complexity limit. This lower bound is tight and demonstrates the optimality of Freya PAGE in the large-scale regime, i.e., when $\sqrt{m} \geq n$, where $n$ is # of workers, and $m$ is # of data samples.

Improving the Worst-Case Bidirectional Communication Complexity for Nonconvex Distributed Optimization under Function Similarity

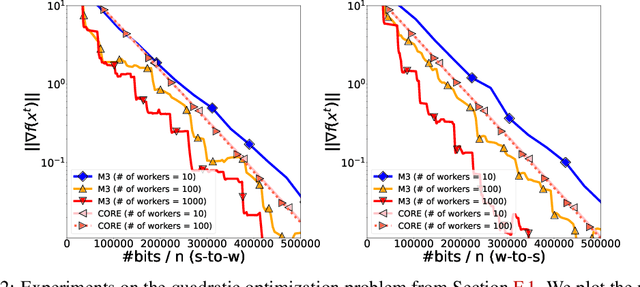
Effective communication between the server and workers plays a key role in distributed optimization. In this paper, we focus on optimizing the server-to-worker communication, uncovering inefficiencies in prevalent downlink compression approaches. Considering first the pure setup where the uplink communication costs are negligible, we introduce MARINA-P, a novel method for downlink compression, employing a collection of correlated compressors. Theoretical analyses demonstrates that MARINA-P with permutation compressors can achieve a server-to-worker communication complexity improving with the number of workers, thus being provably superior to existing algorithms. We further show that MARINA-P can serve as a starting point for extensions such as methods supporting bidirectional compression. We introduce M3, a method combining MARINA-P with uplink compression and a momentum step, achieving bidirectional compression with provable improvements in total communication complexity as the number of workers increases. Theoretical findings align closely with empirical experiments, underscoring the efficiency of the proposed algorithms.

Shadowheart SGD: Distributed Asynchronous SGD with Optimal Time Complexity Under Arbitrary Computation and Communication Heterogeneity

We consider nonconvex stochastic optimization problems in the asynchronous centralized distributed setup where the communication times from workers to a server can not be ignored, and the computation and communication times are potentially different for all workers. Using an unbiassed compression technique, we develop a new method-Shadowheart SGD-that provably improves the time complexities of all previous centralized methods. Moreover, we show that the time complexity of Shadowheart SGD is optimal in the family of centralized methods with compressed communication. We also consider the bidirectional setup, where broadcasting from the server to the workers is non-negligible, and develop a corresponding method.

Momentum Provably Improves Error Feedback!

Due to the high communication overhead when training machine learning models in a distributed environment, modern algorithms invariably rely on lossy communication compression. However, when untreated, the errors caused by compression propagate, and can lead to severely unstable behavior, including exponential divergence. Almost a decade ago, Seide et al [2014] proposed an error feedback (EF) mechanism, which we refer to as EF14, as an immensely effective heuristic for mitigating this issue. However, despite steady algorithmic and theoretical advances in the EF field in the last decade, our understanding is far from complete. In this work we address one of the most pressing issues. In particular, in the canonical nonconvex setting, all known variants of EF rely on very large batch sizes to converge, which can be prohibitive in practice. We propose a surprisingly simple fix which removes this issue both theoretically, and in practice: the application of Polyak's momentum to the latest incarnation of EF due to Richt\'{a}rik et al. [2021] known as EF21. Our algorithm, for which we coin the name EF21-SGDM, improves the communication and sample complexities of previous error feedback algorithms under standard smoothness and bounded variance assumptions, and does not require any further strong assumptions such as bounded gradient dissimilarity. Moreover, we propose a double momentum version of our method that improves the complexities even further. Our proof seems to be novel even when compression is removed from the method, and as such, our proof technique is of independent interest in the study of nonconvex stochastic optimization enriched with Polyak's momentum.