The Ball-Proximal (="Broximal") Point Method: a New Algorithm, Convergence Theory, and Applications

Non-smooth and non-convex global optimization poses significant challenges across various applications, where standard gradient-based methods often struggle. We propose the Ball-Proximal Point Method, Broximal Point Method, or Ball Point Method (BPM) for short - a novel algorithmic framework inspired by the classical Proximal Point Method (PPM) (Rockafellar, 1976), which, as we show, sheds new light on several foundational optimization paradigms and phenomena, including non-convex and non-smooth optimization, acceleration, smoothing, adaptive stepsize selection, and trust-region methods. At the core of BPM lies the ball-proximal ("broximal") operator, which arises from the classical proximal operator by replacing the quadratic distance penalty by a ball constraint. Surprisingly, and in sharp contrast with the sublinear rate of PPM in the nonsmooth convex regime, we prove that BPM converges linearly and in a finite number of steps in the same regime. Furthermore, by introducing the concept of ball-convexity, we prove that BPM retains the same global convergence guarantees under weaker assumptions, making it a powerful tool for a broader class of potentially non-convex optimization problems. Just like PPM plays the role of a conceptual method inspiring the development of practically efficient algorithms and algorithmic elements, e.g., gradient descent, adaptive step sizes, acceleration (Ahn & Sra, 2020), and "W" in AdamW (Zhuang et al., 2022), we believe that BPM should be understood in the same manner: as a blueprint and inspiration for further development.

Tighter Performance Theory of FedExProx

We revisit FedExProx - a recently proposed distributed optimization method designed to enhance convergence properties of parallel proximal algorithms via extrapolation. In the process, we uncover a surprising flaw: its known theoretical guarantees on quadratic optimization tasks are no better than those offered by the vanilla Gradient Descent (GD) method. Motivated by this observation, we develop a novel analysis framework, establishing a tighter linear convergence rate for non-strongly convex quadratic problems. By incorporating both computation and communication costs, we demonstrate that FedExProx can indeed provably outperform GD, in stark contrast to the original analysis. Furthermore, we consider partial participation scenarios and analyze two adaptive extrapolation strategies - based on gradient diversity and Polyak stepsizes - again significantly outperforming previous results. Moving beyond quadratics, we extend the applicability of our analysis to general functions satisfying the Polyak-Lojasiewicz condition, outperforming the previous strongly convex analysis while operating under weaker assumptions. Backed by empirical results, our findings point to a new and stronger potential of FedExProx, paving the way for further exploration of the benefits of extrapolation in federated learning.

Freya PAGE: First Optimal Time Complexity for Large-Scale Nonconvex Finite-Sum Optimization with Heterogeneous Asynchronous Computations

In practical distributed systems, workers are typically not homogeneous, and due to differences in hardware configurations and network conditions, can have highly varying processing times. We consider smooth nonconvex finite-sum (empirical risk minimization) problems in this setup and introduce a new parallel method, Freya PAGE, designed to handle arbitrarily heterogeneous and asynchronous computations. By being robust to "stragglers" and adaptively ignoring slow computations, Freya PAGE offers significantly improved time complexity guarantees compared to all previous methods, including Asynchronous SGD, Rennala SGD, SPIDER, and PAGE, while requiring weaker assumptions. The algorithm relies on novel generic stochastic gradient collection strategies with theoretical guarantees that can be of interest on their own, and may be used in the design of future optimization methods. Furthermore, we establish a lower bound for smooth nonconvex finite-sum problems in the asynchronous setup, providing a fundamental time complexity limit. This lower bound is tight and demonstrates the optimality of Freya PAGE in the large-scale regime, i.e., when $\sqrt{m} \geq n$, where $n$ is # of workers, and $m$ is # of data samples.

Improving the Worst-Case Bidirectional Communication Complexity for Nonconvex Distributed Optimization under Function Similarity

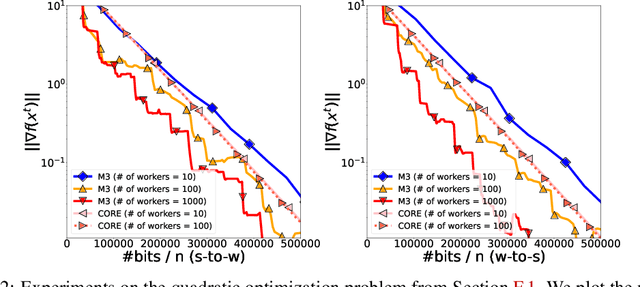
Effective communication between the server and workers plays a key role in distributed optimization. In this paper, we focus on optimizing the server-to-worker communication, uncovering inefficiencies in prevalent downlink compression approaches. Considering first the pure setup where the uplink communication costs are negligible, we introduce MARINA-P, a novel method for downlink compression, employing a collection of correlated compressors. Theoretical analyses demonstrates that MARINA-P with permutation compressors can achieve a server-to-worker communication complexity improving with the number of workers, thus being provably superior to existing algorithms. We further show that MARINA-P can serve as a starting point for extensions such as methods supporting bidirectional compression. We introduce M3, a method combining MARINA-P with uplink compression and a momentum step, achieving bidirectional compression with provable improvements in total communication complexity as the number of workers increases. Theoretical findings align closely with empirical experiments, underscoring the efficiency of the proposed algorithms.

Communication Compression for Byzantine Robust Learning: New Efficient Algorithms and Improved Rates

Byzantine robustness is an essential feature of algorithms for certain distributed optimization problems, typically encountered in collaborative/federated learning. These problems are usually huge-scale, implying that communication compression is also imperative for their resolution. These factors have spurred recent algorithmic and theoretical developments in the literature of Byzantine-robust learning with compression. In this paper, we contribute to this research area in two main directions. First, we propose a new Byzantine-robust method with compression -- Byz-DASHA-PAGE -- and prove that the new method has better convergence rate (for non-convex and Polyak-Lojasiewicz smooth optimization problems), smaller neighborhood size in the heterogeneous case, and tolerates more Byzantine workers under over-parametrization than the previous method with SOTA theoretical convergence guarantees (Byz-VR-MARINA). Secondly, we develop the first Byzantine-robust method with communication compression and error feedback -- Byz-EF21 -- along with its bidirectional compression version -- Byz-EF21-BC -- and derive the convergence rates for these methods for non-convex and Polyak-Lojasiewicz smooth case. We test the proposed methods and illustrate our theoretical findings in the numerical experiments.