Improved Stein Variational Gradient Descent with Importance Weights

Stein Variational Gradient Descent (SVGD) is a popular sampling algorithm used in various machine learning tasks. It is well known that SVGD arises from a discretization of the kernelized gradient flow of the Kullback-Leibler divergence $D_{KL}\left(\cdot\mid\pi\right)$, where $\pi$ is the target distribution. In this work, we propose to enhance SVGD via the introduction of importance weights, which leads to a new method for which we coin the name $\beta$-SVGD. In the continuous time and infinite particles regime, the time for this flow to converge to the equilibrium distribution $\pi$, quantified by the Stein Fisher information, depends on $\rho_0$ and $\pi$ very weakly. This is very different from the kernelized gradient flow of Kullback-Leibler divergence, whose time complexity depends on $D_{KL}\left(\rho_0\mid\pi\right)$. Under certain assumptions, we provide a descent lemma for the population limit $\beta$-SVGD, which covers the descent lemma for the population limit SVGD when $\beta\to 0$. We also illustrate the advantages of $\beta$-SVGD over SVGD by simple experiments.

A Note on the Convergence of Mirrored Stein Variational Gradient Descent under $-$Smoothness Condition

In this note, we establish a descent lemma for the population limit Mirrored Stein Variational Gradient Method~(MSVGD). This descent lemma does not rely on the path information of MSVGD but rather on a simple assumption for the mirrored distribution $\nabla\Psi_{\#}\pi\propto\exp(-V)$. Our analysis demonstrates that MSVGD can be applied to a broader class of constrained sampling problems with non-smooth $V$. We also investigate the complexity of the population limit MSVGD in terms of dimension $d$.

Federated Learning with a Sampling Algorithm under Isoperimetry

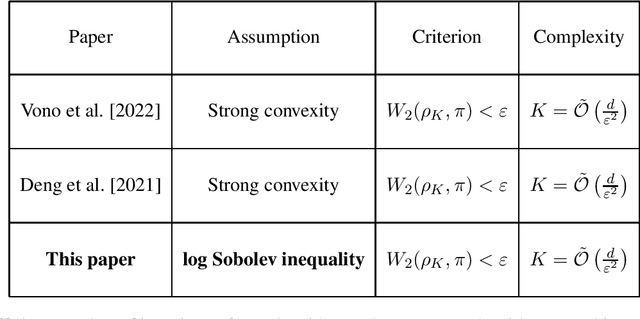
Federated learning uses a set of techniques to efficiently distribute the training of a machine learning algorithm across several devices, who own the training data. These techniques critically rely on reducing the communication cost -- the main bottleneck -- between the devices and a central server. Federated learning algorithms usually take an optimization approach: they are algorithms for minimizing the training loss subject to communication (and other) constraints. In this work, we instead take a Bayesian approach for the training task, and propose a communication-efficient variant of the Langevin algorithm to sample a posteriori. The latter approach is more robust and provides more knowledge of the \textit{a posteriori} distribution than its optimization counterpart. We analyze our algorithm without assuming that the target distribution is strongly log-concave. Instead, we assume the weaker log Sobolev inequality, which allows for nonconvexity.

Sharper Rates and Flexible Framework for Nonconvex SGD with Client and Data Sampling

We revisit the classical problem of finding an approximately stationary point of the average of $n$ smooth and possibly nonconvex functions. The optimal complexity of stochastic first-order methods in terms of the number of gradient evaluations of individual functions is $\mathcal{O}\left(n + n^{1/2}\varepsilon^{-1}\right)$, attained by the optimal SGD methods $\small\sf\color{green}{SPIDER}$(arXiv:1807.01695) and $\small\sf\color{green}{PAGE}$(arXiv:2008.10898), for example, where $\varepsilon$ is the error tolerance. However, i) the big-$\mathcal{O}$ notation hides crucial dependencies on the smoothness constants associated with the functions, and ii) the rates and theory in these methods assume simplistic sampling mechanisms that do not offer any flexibility. In this work we remedy the situation. First, we generalize the $\small\sf\color{green}{PAGE}$ algorithm so that it can provably work with virtually any (unbiased) sampling mechanism. This is particularly useful in federated learning, as it allows us to construct and better understand the impact of various combinations of client and data sampling strategies. Second, our analysis is sharper as we make explicit use of certain novel inequalities that capture the intricate interplay between the smoothness constants and the sampling procedure. Indeed, our analysis is better even for the simple sampling procedure analyzed in the $\small\sf\color{green}{PAGE}$ paper. However, this already improved bound can be further sharpened by a different sampling scheme which we propose. In summary, we provide the most general and most accurate analysis of optimal SGD in the smooth nonconvex regime. Finally, our theoretical findings are supposed with carefully designed experiments.

Convergence of Stein Variational Gradient Descent under a Weaker Smoothness Condition

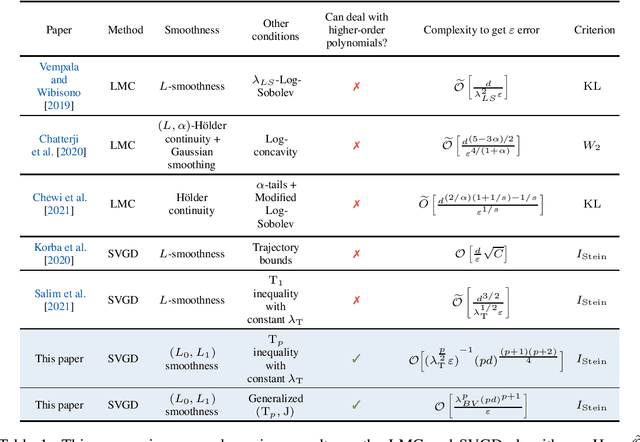
Stein Variational Gradient Descent (SVGD) is an important alternative to the Langevin-type algorithms for sampling from probability distributions of the form $\pi(x) \propto \exp(-V(x))$. In the existing theory of Langevin-type algorithms and SVGD, the potential function $V$ is often assumed to be $L$-smooth. However, this restrictive condition excludes a large class of potential functions such as polynomials of degree greater than $2$. Our paper studies the convergence of the SVGD algorithm for distributions with $(L_0,L_1)$-smooth potentials. This relaxed smoothness assumption was introduced by Zhang et al. [2019a] for the analysis of gradient clipping algorithms. With the help of trajectory-independent auxiliary conditions, we provide a descent lemma establishing that the algorithm decreases the $\mathrm{KL}$ divergence at each iteration and prove a complexity bound for SVGD in the population limit in terms of the Stein Fisher information.

Complexity Analysis of Stein Variational Gradient Descent Under Talagrand's Inequality T1

We study the complexity of Stein Variational Gradient Descent (SVGD), which is an algorithm to sample from $\pi(x) \propto \exp(-F(x))$ where $F$ smooth and nonconvex. We provide a clean complexity bound for SVGD in the population limit in terms of the Stein Fisher Information (or squared Kernelized Stein Discrepancy), as a function of the dimension of the problem $d$ and the desired accuracy $\varepsilon$. Unlike existing work, we do not make any assumption on the trajectory of the algorithm. Instead, our key assumption is that the target distribution satisfies Talagrand's inequality T1.