Convergence of Stein Variational Gradient Descent under a Weaker Smoothness Condition
Paper and Code
Jun 01, 2022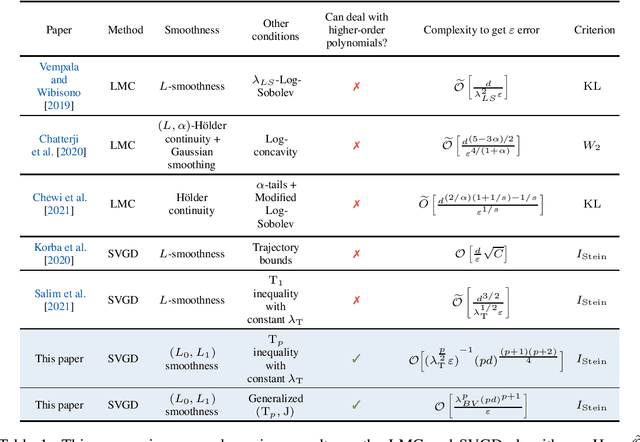
Stein Variational Gradient Descent (SVGD) is an important alternative to the Langevin-type algorithms for sampling from probability distributions of the form $\pi(x) \propto \exp(-V(x))$. In the existing theory of Langevin-type algorithms and SVGD, the potential function $V$ is often assumed to be $L$-smooth. However, this restrictive condition excludes a large class of potential functions such as polynomials of degree greater than $2$. Our paper studies the convergence of the SVGD algorithm for distributions with $(L_0,L_1)$-smooth potentials. This relaxed smoothness assumption was introduced by Zhang et al. [2019a] for the analysis of gradient clipping algorithms. With the help of trajectory-independent auxiliary conditions, we provide a descent lemma establishing that the algorithm decreases the $\mathrm{KL}$ divergence at each iteration and prove a complexity bound for SVGD in the population limit in terms of the Stein Fisher information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge