SPAM: Stochastic Proximal Point Method with Momentum Variance Reduction for Non-convex Cross-Device Federated Learning

Cross-device training is a crucial subfield of federated learning, where the number of clients can reach into the billions. Standard approaches and local methods are prone to issues such as client drift and insensitivity to data similarities. We propose a novel algorithm (SPAM) for cross-device federated learning with non-convex losses, which solves both issues. We provide sharp analysis under second-order (Hessian) similarity, a condition satisfied by a variety of machine learning problems in practice. Additionally, we extend our results to the partial participation setting, where a cohort of selected clients communicate with the server at each communication round. Our method is the first in its kind, that does not require the smoothness of the objective and provably benefits from clients having similar data.

Applying statistical learning theory to deep learning

Although statistical learning theory provides a robust framework to understand supervised learning, many theoretical aspects of deep learning remain unclear, in particular how different architectures may lead to inductive bias when trained using gradient based methods. The goal of these lectures is to provide an overview of some of the main questions that arise when attempting to understand deep learning from a learning theory perspective. After a brief reminder on statistical learning theory and stochastic optimization, we discuss implicit bias in the context of benign overfitting. We then move to a general description of the mirror descent algorithm, showing how we may go back and forth between a parameter space and the corresponding function space for a given learning problem, as well as how the geometry of the learning problem may be represented by a metric tensor. Building on this framework, we provide a detailed study of the implicit bias of gradient descent on linear diagonal networks for various regression tasks, showing how the loss function, scale of parameters at initialization and depth of the network may lead to various forms of implicit bias, in particular transitioning between kernel or feature learning.

Langevin Monte Carlo for strongly log-concave distributions: Randomized midpoint revisited

We revisit the problem of sampling from a target distribution that has a smooth strongly log-concave density everywhere in $\mathbb R^p$. In this context, if no additional density information is available, the randomized midpoint discretization for the kinetic Langevin diffusion is known to be the most scalable method in high dimensions with large condition numbers. Our main result is a nonasymptotic and easy to compute upper bound on the Wasserstein-2 error of this method. To provide a more thorough explanation of our method for establishing the computable upper bound, we conduct an analysis of the midpoint discretization for the vanilla Langevin process. This analysis helps to clarify the underlying principles and provides valuable insights that we use to establish an improved upper bound for the kinetic Langevin process with the midpoint discretization. Furthermore, by applying these techniques we establish new guarantees for the kinetic Langevin process with Euler discretization, which have a better dependence on the condition number than existing upper bounds.

ELF: Federated Langevin Algorithms with Primal, Dual and Bidirectional Compression

Federated sampling algorithms have recently gained great popularity in the community of machine learning and statistics. This paper studies variants of such algorithms called Error Feedback Langevin algorithms (ELF). In particular, we analyze the combinations of EF21 and EF21-P with the federated Langevin Monte-Carlo. We propose three algorithms: P-ELF, D-ELF, and B-ELF that use, respectively, primal, dual, and bidirectional compressors. We analyze the proposed methods under Log-Sobolev inequality and provide non-asymptotic convergence guarantees.

Convergence of Stein Variational Gradient Descent under a Weaker Smoothness Condition

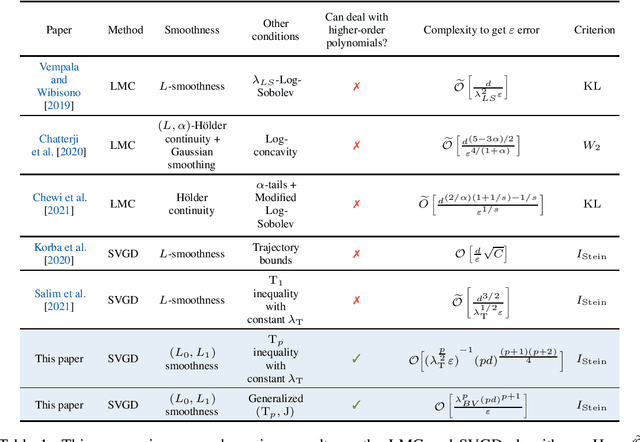
Stein Variational Gradient Descent (SVGD) is an important alternative to the Langevin-type algorithms for sampling from probability distributions of the form $\pi(x) \propto \exp(-V(x))$. In the existing theory of Langevin-type algorithms and SVGD, the potential function $V$ is often assumed to be $L$-smooth. However, this restrictive condition excludes a large class of potential functions such as polynomials of degree greater than $2$. Our paper studies the convergence of the SVGD algorithm for distributions with $(L_0,L_1)$-smooth potentials. This relaxed smoothness assumption was introduced by Zhang et al. [2019a] for the analysis of gradient clipping algorithms. With the help of trajectory-independent auxiliary conditions, we provide a descent lemma establishing that the algorithm decreases the $\mathrm{KL}$ divergence at each iteration and prove a complexity bound for SVGD in the population limit in terms of the Stein Fisher information.

Penalized Langevin dynamics with vanishing penalty for smooth and log-concave targets

We study the problem of sampling from a probability distribution on $\mathbb R^p$ defined via a convex and smooth potential function. We consider a continuous-time diffusion-type process, termed Penalized Langevin dynamics (PLD), the drift of which is the negative gradient of the potential plus a linear penalty that vanishes when time goes to infinity. An upper bound on the Wasserstein-2 distance between the distribution of the PLD at time $t$ and the target is established. This upper bound highlights the influence of the speed of decay of the penalty on the accuracy of the approximation. As a consequence, considering the low-temperature limit we infer a new nonasymptotic guarantee of convergence of the penalized gradient flow for the optimization problem.

Bounding the error of discretized Langevin algorithms for non-strongly log-concave targets

In this paper, we provide non-asymptotic upper bounds on the error of sampling from a target density using three schemes of discretized Langevin diffusions. The first scheme is the Langevin Monte Carlo (LMC) algorithm, the Euler discretization of the Langevin diffusion. The second and the third schemes are, respectively, the kinetic Langevin Monte Carlo (KLMC) for differentiable potentials and the kinetic Langevin Monte Carlo for twice-differentiable potentials (KLMC2). The main focus is on the target densities that are smooth and log-concave on $\RR^p$, but not necessarily strongly log-concave. Bounds on the computational complexity are obtained under two types of smoothness assumption: the potential has a Lipschitz-continuous gradient and the potential has a Lipschitz-continuous Hessian matrix. The error of sampling is measured by Wasserstein-$q$ distances and the bounded-Lipschitz distance. We advocate for the use of a new dimension-adapted scaling in the definition of the computational complexity, when Wasserstein-$q$ distances are considered. The obtained results show that the number of iterations to achieve a scaled-error smaller than a prescribed value depends only polynomially in the dimension.