Applying statistical learning theory to deep learning

Although statistical learning theory provides a robust framework to understand supervised learning, many theoretical aspects of deep learning remain unclear, in particular how different architectures may lead to inductive bias when trained using gradient based methods. The goal of these lectures is to provide an overview of some of the main questions that arise when attempting to understand deep learning from a learning theory perspective. After a brief reminder on statistical learning theory and stochastic optimization, we discuss implicit bias in the context of benign overfitting. We then move to a general description of the mirror descent algorithm, showing how we may go back and forth between a parameter space and the corresponding function space for a given learning problem, as well as how the geometry of the learning problem may be represented by a metric tensor. Building on this framework, we provide a detailed study of the implicit bias of gradient descent on linear diagonal networks for various regression tasks, showing how the loss function, scale of parameters at initialization and depth of the network may lead to various forms of implicit bias, in particular transitioning between kernel or feature learning.

Machine Learning Without a Processor: Emergent Learning in a Nonlinear Electronic Metamaterial

Standard deep learning algorithms require differentiating large nonlinear networks, a process that is slow and power-hungry. Electronic learning metamaterials offer potentially fast, efficient, and fault-tolerant hardware for analog machine learning, but existing implementations are linear, severely limiting their capabilities. These systems differ significantly from artificial neural networks as well as the brain, so the feasibility and utility of incorporating nonlinear elements have not been explored. Here we introduce a nonlinear learning metamaterial -- an analog electronic network made of self-adjusting nonlinear resistive elements based on transistors. We demonstrate that the system learns tasks unachievable in linear systems, including XOR and nonlinear regression, without a computer. We find our nonlinear learning metamaterial reduces modes of training error in order (mean, slope, curvature), similar to spectral bias in artificial neural networks. The circuitry is robust to damage, retrainable in seconds, and performs learned tasks in microseconds while dissipating only picojoules of energy across each transistor. This suggests enormous potential for fast, low-power computing in edge systems like sensors, robotic controllers, and medical devices, as well as manufacturability at scale for performing and studying emergent learning.

Learning Without a Global Clock: Asynchronous Learning in a Physics-Driven Learning Network

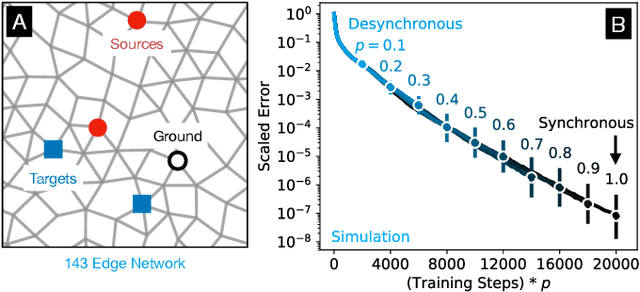
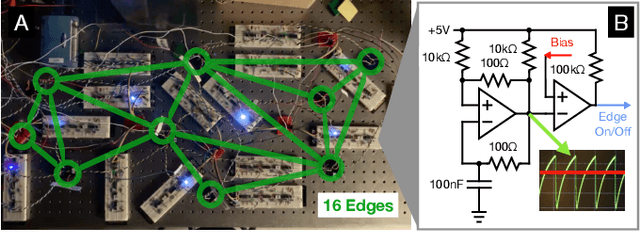
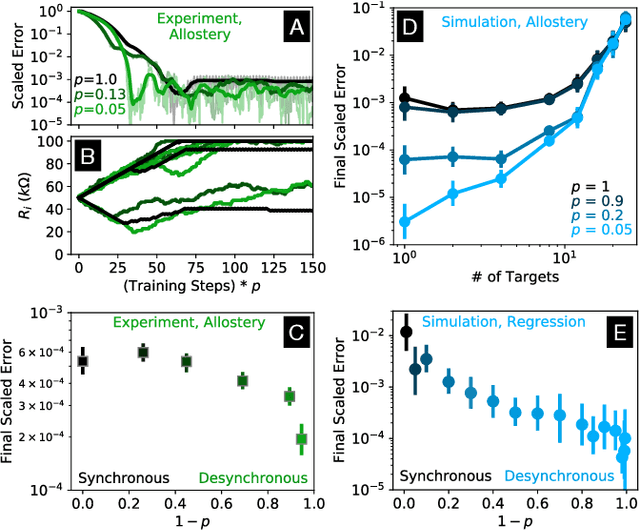
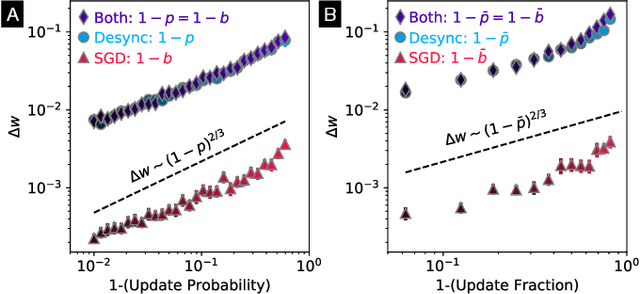
In a neuron network, synapses update individually using local information, allowing for entirely decentralized learning. In contrast, elements in an artificial neural network (ANN) are typically updated simultaneously using a central processor. Here we investigate the feasibility and effect of asynchronous learning in a recently introduced decentralized, physics-driven learning network. We show that desynchronizing the learning process does not degrade performance for a variety of tasks in an idealized simulation. In experiment, desynchronization actually improves performance by allowing the system to better explore the discretized state space of solutions. We draw an analogy between asynchronicity and mini-batching in stochastic gradient descent, and show that they have similar effects on the learning process. Desynchronizing the learning process establishes physics-driven learning networks as truly fully distributed learning machines, promoting better performance and scalability in deployment.