Gemini Robotics: Bringing AI into the Physical World

Recent advancements in large multimodal models have led to the emergence of remarkable generalist capabilities in digital domains, yet their translation to physical agents such as robots remains a significant challenge. This report introduces a new family of AI models purposefully designed for robotics and built upon the foundation of Gemini 2.0. We present Gemini Robotics, an advanced Vision-Language-Action (VLA) generalist model capable of directly controlling robots. Gemini Robotics executes smooth and reactive movements to tackle a wide range of complex manipulation tasks while also being robust to variations in object types and positions, handling unseen environments as well as following diverse, open vocabulary instructions. We show that with additional fine-tuning, Gemini Robotics can be specialized to new capabilities including solving long-horizon, highly dexterous tasks, learning new short-horizon tasks from as few as 100 demonstrations and adapting to completely novel robot embodiments. This is made possible because Gemini Robotics builds on top of the Gemini Robotics-ER model, the second model we introduce in this work. Gemini Robotics-ER (Embodied Reasoning) extends Gemini's multimodal reasoning capabilities into the physical world, with enhanced spatial and temporal understanding. This enables capabilities relevant to robotics including object detection, pointing, trajectory and grasp prediction, as well as multi-view correspondence and 3D bounding box predictions. We show how this novel combination can support a variety of robotics applications. We also discuss and address important safety considerations related to this new class of robotics foundation models. The Gemini Robotics family marks a substantial step towards developing general-purpose robots that realizes AI's potential in the physical world.

On the Inductive Bias of Stacking Towards Improving Reasoning

Given the increasing scale of model sizes, novel training strategies like gradual stacking [Gong et al., 2019, Reddi et al., 2023] have garnered interest. Stacking enables efficient training by gradually growing the depth of a model in stages and using layers from a smaller model in an earlier stage to initialize the next stage. Although efficient for training, the model biases induced by such growing approaches are largely unexplored. In this work, we examine this fundamental aspect of gradual stacking, going beyond its efficiency benefits. We propose a variant of gradual stacking called MIDAS that can speed up language model training by up to 40%. Furthermore we discover an intriguing phenomenon: MIDAS is not only training-efficient but surprisingly also has an inductive bias towards improving downstream tasks, especially tasks that require reasoning abilities like reading comprehension and math problems, despite having similar or slightly worse perplexity compared to baseline training. To further analyze this inductive bias, we construct reasoning primitives -- simple synthetic tasks that are building blocks for reasoning -- and find that a model pretrained with stacking is significantly better than standard pretraining on these primitives, with and without fine-tuning. This provides stronger and more robust evidence for this inductive bias towards reasoning. These findings of training efficiency and inductive bias towards reasoning are verified at 1B, 2B and 8B parameter language models. Finally, we conjecture the underlying reason for this inductive bias by exploring the connection of stacking to looped models and provide strong supporting empirical analysis.

Landscape-Aware Growing: The Power of a Little LAG

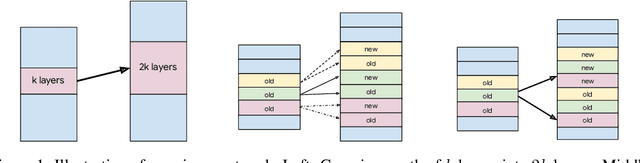
Recently, there has been increasing interest in efficient pretraining paradigms for training Transformer-based models. Several recent approaches use smaller models to initialize larger models in order to save computation (e.g., stacking and fusion). In this work, we study the fundamental question of how to select the best growing strategy from a given pool of growing strategies. Prior works have extensively focused on loss- and/or function-preserving behavior at initialization or simply performance at the end of training. Instead, we identify that behavior at initialization can be misleading as a predictor of final performance and present an alternative perspective based on early training dynamics, which we call "landscape-aware growing (LAG)". We perform extensive analysis of correlation of the final performance with performance in the initial steps of training and find early and more accurate predictions of the optimal growing strategy (i.e., with only a small "lag" after initialization). This perspective also motivates an adaptive strategy for gradual stacking.

Role of Locality and Weight Sharing in Image-Based Tasks: A Sample Complexity Separation between CNNs, LCNs, and FCNs

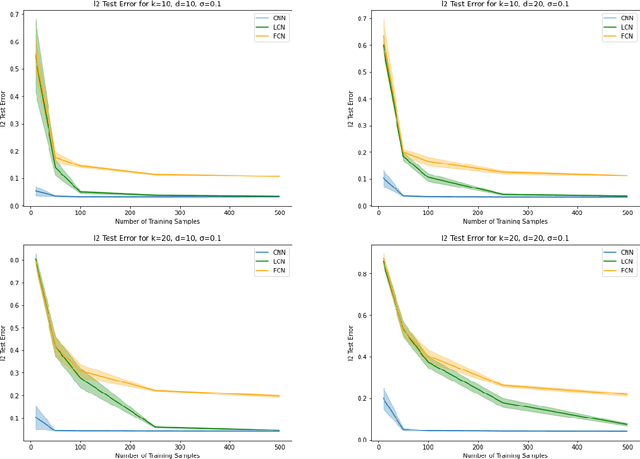
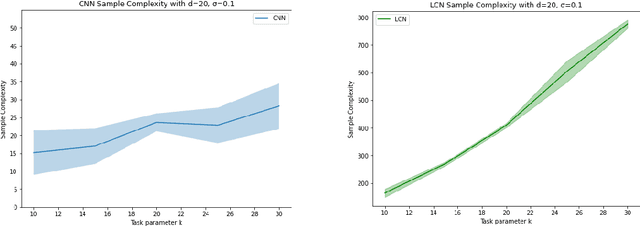
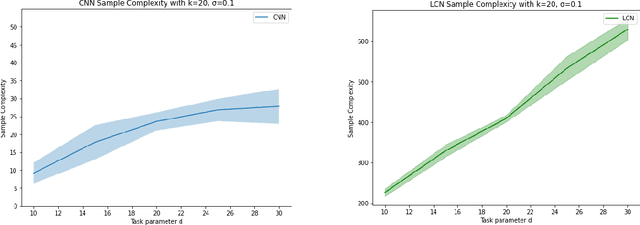
Vision tasks are characterized by the properties of locality and translation invariance. The superior performance of convolutional neural networks (CNNs) on these tasks is widely attributed to the inductive bias of locality and weight sharing baked into their architecture. Existing attempts to quantify the statistical benefits of these biases in CNNs over locally connected convolutional neural networks (LCNs) and fully connected neural networks (FCNs) fall into one of the following categories: either they disregard the optimizer and only provide uniform convergence upper bounds with no separating lower bounds, or they consider simplistic tasks that do not truly mirror the locality and translation invariance as found in real-world vision tasks. To address these deficiencies, we introduce the Dynamic Signal Distribution (DSD) classification task that models an image as consisting of $k$ patches, each of dimension $d$, and the label is determined by a $d$-sparse signal vector that can freely appear in any one of the $k$ patches. On this task, for any orthogonally equivariant algorithm like gradient descent, we prove that CNNs require $\tilde{O}(k+d)$ samples, whereas LCNs require $\Omega(kd)$ samples, establishing the statistical advantages of weight sharing in translation invariant tasks. Furthermore, LCNs need $\tilde{O}(k(k+d))$ samples, compared to $\Omega(k^2d)$ samples for FCNs, showcasing the benefits of locality in local tasks. Additionally, we develop information theoretic tools for analyzing randomized algorithms, which may be of interest for statistical research.

Applying statistical learning theory to deep learning

Although statistical learning theory provides a robust framework to understand supervised learning, many theoretical aspects of deep learning remain unclear, in particular how different architectures may lead to inductive bias when trained using gradient based methods. The goal of these lectures is to provide an overview of some of the main questions that arise when attempting to understand deep learning from a learning theory perspective. After a brief reminder on statistical learning theory and stochastic optimization, we discuss implicit bias in the context of benign overfitting. We then move to a general description of the mirror descent algorithm, showing how we may go back and forth between a parameter space and the corresponding function space for a given learning problem, as well as how the geometry of the learning problem may be represented by a metric tensor. Building on this framework, we provide a detailed study of the implicit bias of gradient descent on linear diagonal networks for various regression tasks, showing how the loss function, scale of parameters at initialization and depth of the network may lead to various forms of implicit bias, in particular transitioning between kernel or feature learning.

Agnostic Learnability of Halfspaces via Logistic Loss

We investigate approximation guarantees provided by logistic regression for the fundamental problem of agnostic learning of homogeneous halfspaces. Previously, for a certain broad class of "well-behaved" distributions on the examples, Diakonikolas et al. (2020) proved an $\tilde{\Omega}(\textrm{OPT})$ lower bound, while Frei et al. (2021) proved an $\tilde{O}(\sqrt{\textrm{OPT}})$ upper bound, where $\textrm{OPT}$ denotes the best zero-one/misclassification risk of a homogeneous halfspace. In this paper, we close this gap by constructing a well-behaved distribution such that the global minimizer of the logistic risk over this distribution only achieves $\Omega(\sqrt{\textrm{OPT}})$ misclassification risk, matching the upper bound in (Frei et al., 2021). On the other hand, we also show that if we impose a radial-Lipschitzness condition in addition to well-behaved-ness on the distribution, logistic regression on a ball of bounded radius reaches $\tilde{O}(\textrm{OPT})$ misclassification risk. Our techniques also show for any well-behaved distribution, regardless of radial Lipschitzness, we can overcome the $\Omega(\sqrt{\textrm{OPT}})$ lower bound for logistic loss simply at the cost of one additional convex optimization step involving the hinge loss and attain $\tilde{O}(\textrm{OPT})$ misclassification risk. This two-step convex optimization algorithm is simpler than previous methods obtaining this guarantee, all of which require solving $O(\log(1/\textrm{OPT}))$ minimization problems.