Role of Locality and Weight Sharing in Image-Based Tasks: A Sample Complexity Separation between CNNs, LCNs, and FCNs

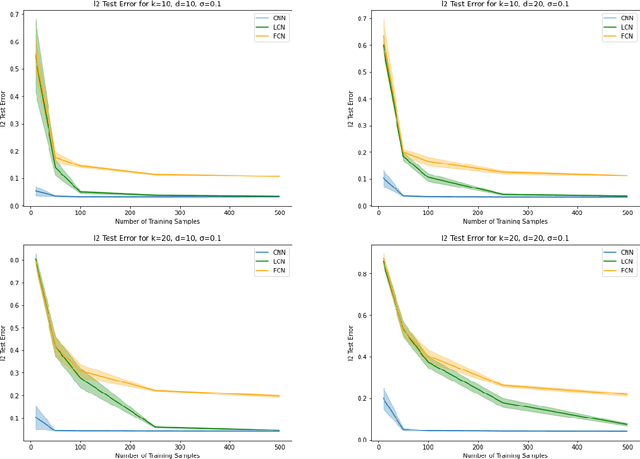
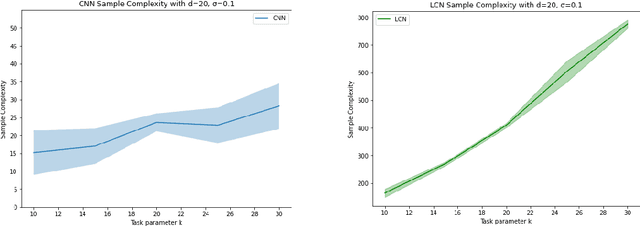
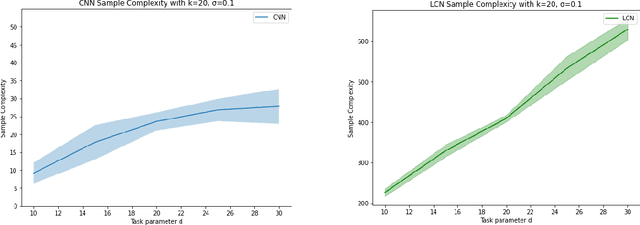
Vision tasks are characterized by the properties of locality and translation invariance. The superior performance of convolutional neural networks (CNNs) on these tasks is widely attributed to the inductive bias of locality and weight sharing baked into their architecture. Existing attempts to quantify the statistical benefits of these biases in CNNs over locally connected convolutional neural networks (LCNs) and fully connected neural networks (FCNs) fall into one of the following categories: either they disregard the optimizer and only provide uniform convergence upper bounds with no separating lower bounds, or they consider simplistic tasks that do not truly mirror the locality and translation invariance as found in real-world vision tasks. To address these deficiencies, we introduce the Dynamic Signal Distribution (DSD) classification task that models an image as consisting of $k$ patches, each of dimension $d$, and the label is determined by a $d$-sparse signal vector that can freely appear in any one of the $k$ patches. On this task, for any orthogonally equivariant algorithm like gradient descent, we prove that CNNs require $\tilde{O}(k+d)$ samples, whereas LCNs require $\Omega(kd)$ samples, establishing the statistical advantages of weight sharing in translation invariant tasks. Furthermore, LCNs need $\tilde{O}(k(k+d))$ samples, compared to $\Omega(k^2d)$ samples for FCNs, showcasing the benefits of locality in local tasks. Additionally, we develop information theoretic tools for analyzing randomized algorithms, which may be of interest for statistical research.

Monotone deep Boltzmann machines

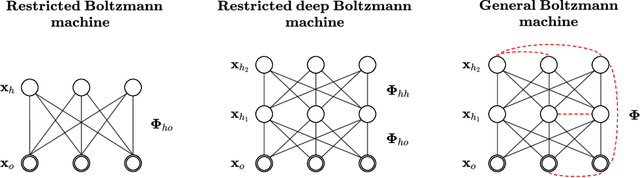
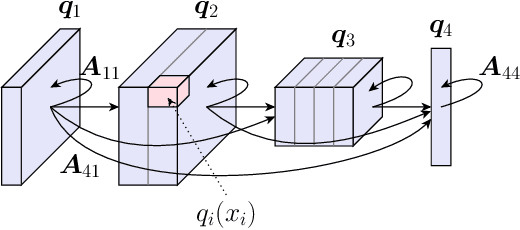
Deep Boltzmann machines (DBMs), one of the first ``deep'' learning methods ever studied, are multi-layered probabilistic models governed by a pairwise energy function that describes the likelihood of all variables/nodes in the network. In practice, DBMs are often constrained, i.e., via the \emph{restricted} Boltzmann machine (RBM) architecture (which does not permit intra-layer connections), in order to allow for more efficient inference. In this work, we revisit the generic DBM approach, and ask the question: are there other possible restrictions to their design that would enable efficient (approximate) inference? In particular, we develop a new class of restricted model, the monotone DBM, which allows for arbitrary self-connection in each layer, but restricts the \emph{weights} in a manner that guarantees the existence and global uniqueness of a mean-field fixed point. To do this, we leverage tools from the recently-proposed monotone Deep Equilibrium model and show that a particular choice of activation results in a fixed-point iteration that gives a variational mean-field solution. While this approach is still largely conceptual, it is the first architecture that allows for efficient approximate inference in fully-general weight structures for DBMs. We apply this approach to simple deep convolutional Boltzmann architectures and demonstrate that it allows for tasks such as the joint completion and classification of images, within a single deep probabilistic setting, while avoiding the pitfalls of mean-field inference in traditional RBMs.

Monotone operator equilibrium networks

Implicit-depth models such as Deep Equilibrium Networks have recently been shown to match or exceed the performance of traditional deep networks while being much more memory efficient. However, these models suffer from unstable convergence to a solution and lack guarantees that a solution exists. On the other hand, Neural ODEs, another class of implicit-depth models, do guarantee existence of a unique solution but perform poorly compared with traditional networks. In this paper, we develop a new class of implicit-depth model based on the theory of monotone operators, the Monotone Operator Equilibrium Network (MON). We show the close connection between finding the equilibrium point of an implicit network and solving a form of monotone operator splitting problem, which admits efficient solvers with guaranteed, stable convergence. We then develop a parameterization of the network which ensures that all operators remain monotone, which guarantees the existence of a unique equilibrium point. Finally, we show how to instantiate several versions of these models, and implement the resulting iterative solvers, for structured linear operators such as multi-scale convolutions. The resulting models vastly outperform the Neural ODE-based models while also being more computationally efficient. Code is available at http://github.com/locuslab/monotone_op_net.

Certified Robustness to Label-Flipping Attacks via Randomized Smoothing

Machine learning algorithms are known to be susceptible to data poisoning attacks, where an adversary manipulates the training data to degrade performance of the resulting classifier. While many heuristic defenses have been proposed, few defenses exist which are certified against worst-case corruption of the training data. In this work, we propose a strategy to build linear classifiers that are certifiably robust against a strong variant of label-flipping, where each test example is targeted independently. In other words, for each test point, our classifier makes a prediction and includes a certification that its prediction would be the same had some number of training labels been changed adversarially. Our approach leverages randomized smoothing, a technique that has previously been used to guarantee---with high probability---test-time robustness to adversarial manipulation of the input to a classifier. We derive a variant which provides a deterministic, analytical bound, sidestepping the probabilistic certificates that traditionally result from the sampling subprocedure. Further, we obtain these certified bounds with no additional runtime cost over standard classification. We generalize our results to the multi-class case, providing what we believe to be the first multi-class classification algorithm that is certifiably robust to label-flipping attacks.

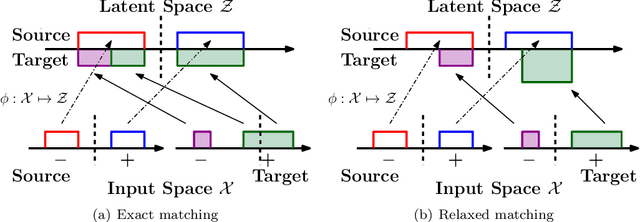
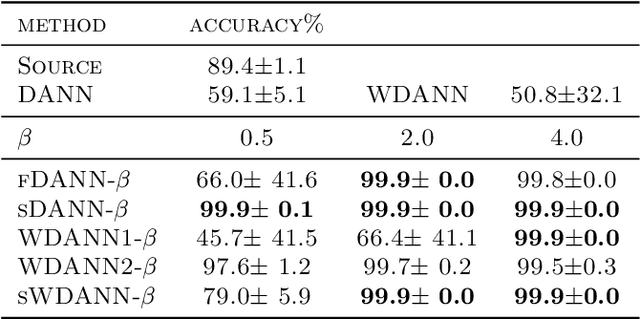
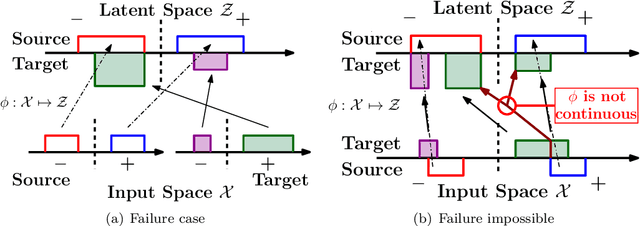
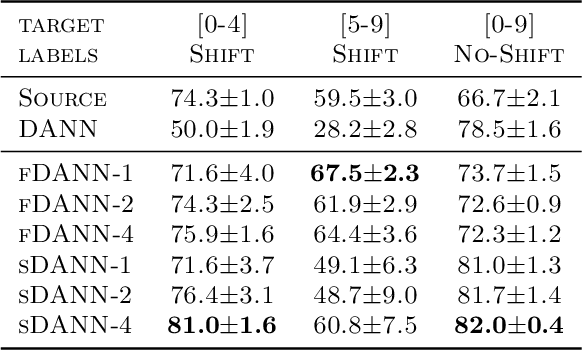
Domain Adaptation with Asymmetrically-Relaxed Distribution Alignment

Domain adaptation addresses the common problem when the target distribution generating our test data drifts from the source (training) distribution. While absent assumptions, domain adaptation is impossible, strict conditions, e.g. covariate or label shift, enable principled algorithms. Recently-proposed domain-adversarial approaches consist of aligning source and target encodings, often motivating this approach as minimizing two (of three) terms in a theoretical bound on target error. Unfortunately, this minimization can cause arbitrary increases in the third term, e.g. they can break down under shifting label distributions. We propose asymmetrically-relaxed distribution alignment, a new approach that overcomes some limitations of standard domain-adversarial algorithms. Moreover, we characterize precise assumptions under which our algorithm is theoretically principled and demonstrate empirical benefits on both synthetic and real datasets.