Monotone deep Boltzmann machines
Paper and Code
Jul 11, 2023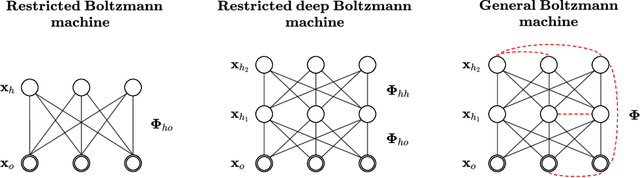

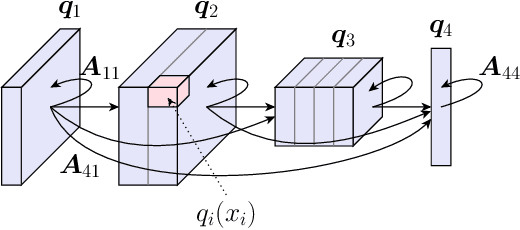

Deep Boltzmann machines (DBMs), one of the first ``deep'' learning methods ever studied, are multi-layered probabilistic models governed by a pairwise energy function that describes the likelihood of all variables/nodes in the network. In practice, DBMs are often constrained, i.e., via the \emph{restricted} Boltzmann machine (RBM) architecture (which does not permit intra-layer connections), in order to allow for more efficient inference. In this work, we revisit the generic DBM approach, and ask the question: are there other possible restrictions to their design that would enable efficient (approximate) inference? In particular, we develop a new class of restricted model, the monotone DBM, which allows for arbitrary self-connection in each layer, but restricts the \emph{weights} in a manner that guarantees the existence and global uniqueness of a mean-field fixed point. To do this, we leverage tools from the recently-proposed monotone Deep Equilibrium model and show that a particular choice of activation results in a fixed-point iteration that gives a variational mean-field solution. While this approach is still largely conceptual, it is the first architecture that allows for efficient approximate inference in fully-general weight structures for DBMs. We apply this approach to simple deep convolutional Boltzmann architectures and demonstrate that it allows for tasks such as the joint completion and classification of images, within a single deep probabilistic setting, while avoiding the pitfalls of mean-field inference in traditional RBMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge