Federated Learning with a Sampling Algorithm under Isoperimetry
Paper and Code
Jun 07, 2022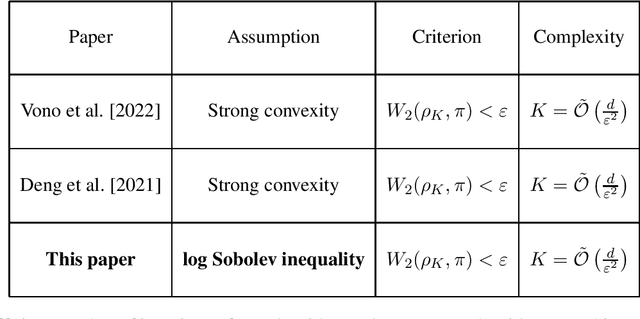
Federated learning uses a set of techniques to efficiently distribute the training of a machine learning algorithm across several devices, who own the training data. These techniques critically rely on reducing the communication cost -- the main bottleneck -- between the devices and a central server. Federated learning algorithms usually take an optimization approach: they are algorithms for minimizing the training loss subject to communication (and other) constraints. In this work, we instead take a Bayesian approach for the training task, and propose a communication-efficient variant of the Langevin algorithm to sample a posteriori. The latter approach is more robust and provides more knowledge of the \textit{a posteriori} distribution than its optimization counterpart. We analyze our algorithm without assuming that the target distribution is strongly log-concave. Instead, we assume the weaker log Sobolev inequality, which allows for nonconvexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge