On the Crucial Role of Initialization for Matrix Factorization
Paper and Code
Oct 24, 2024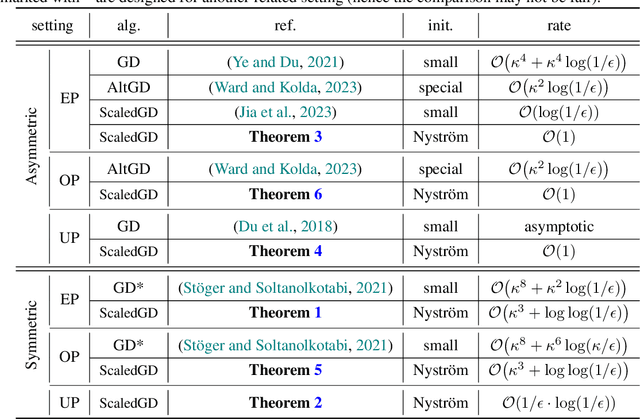


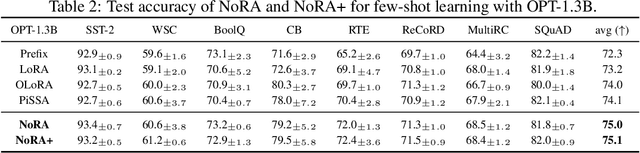
This work revisits the classical low-rank matrix factorization problem and unveils the critical role of initialization in shaping convergence rates for such nonconvex and nonsmooth optimization. We introduce Nystrom initialization, which significantly improves the global convergence of Scaled Gradient Descent (ScaledGD) in both symmetric and asymmetric matrix factorization tasks. Specifically, we prove that ScaledGD with Nystrom initialization achieves quadratic convergence in cases where only linear rates were previously known. Furthermore, we extend this initialization to low-rank adapters (LoRA) commonly used for finetuning foundation models. Our approach, NoRA, i.e., LoRA with Nystrom initialization, demonstrates superior performance across various downstream tasks and model scales, from 1B to 7B parameters, in large language and diffusion models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge