Scaling Laws For Scalable Oversight

Scalable oversight, the process by which weaker AI systems supervise stronger ones, has been proposed as a key strategy to control future superintelligent systems. However, it is still unclear how scalable oversight itself scales. To address this gap, we propose a framework that quantifies the probability of successful oversight as a function of the capabilities of the overseer and the system being overseen. Specifically, our framework models oversight as a game between capability-mismatched players; the players have oversight-specific and deception-specific Elo scores that are a piecewise-linear function of their general intelligence, with two plateaus corresponding to task incompetence and task saturation. We validate our framework with a modified version of the game Nim and then apply it to four oversight games: "Mafia", "Debate", "Backdoor Code" and "Wargames". For each game, we find scaling laws that approximate how domain performance depends on general AI system capability (using Chatbot Arena Elo as a proxy for general capability). We then build on our findings in a theoretical study of Nested Scalable Oversight (NSO), a process in which trusted models oversee untrusted stronger models, which then become the trusted models in the next step. We identify conditions under which NSO succeeds and derive numerically (and in some cases analytically) the optimal number of oversight levels to maximize the probability of oversight success. In our numerical examples, the NSO success rate is below 52% when overseeing systems that are 400 Elo points stronger than the baseline overseer, and it declines further for overseeing even stronger systems.

Towards Understanding Distilled Reasoning Models: A Representational Approach

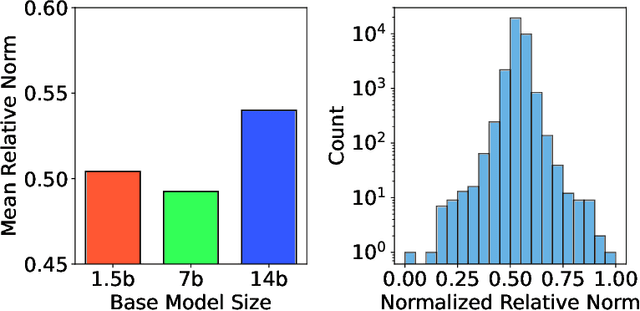
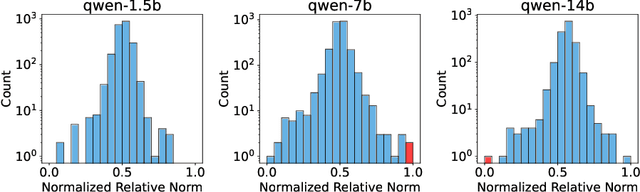
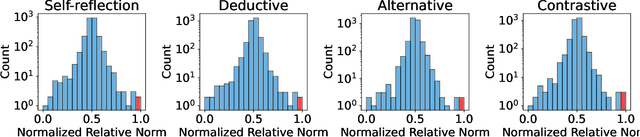
In this paper, we investigate how model distillation impacts the development of reasoning features in large language models (LLMs). To explore this, we train a crosscoder on Qwen-series models and their fine-tuned variants. Our results suggest that the crosscoder learns features corresponding to various types of reasoning, including self-reflection and computation verification. Moreover, we observe that distilled models contain unique reasoning feature directions, which could be used to steer the model into over-thinking or incisive-thinking mode. In particular, we perform analysis on four specific reasoning categories: (a) self-reflection, (b) deductive reasoning, (c) alternative reasoning, and (d) contrastive reasoning. Finally, we examine the changes in feature geometry resulting from the distillation process and find indications that larger distilled models may develop more structured representations, which correlate with enhanced distillation performance. By providing insights into how distillation modifies the model, our study contributes to enhancing the transparency and reliability of AI systems.

Harmonic Loss Trains Interpretable AI Models

In this paper, we introduce **harmonic loss** as an alternative to the standard cross-entropy loss for training neural networks and large language models (LLMs). Harmonic loss enables improved interpretability and faster convergence, owing to its scale invariance and finite convergence point by design, which can be interpreted as a class center. We first validate the performance of harmonic models across algorithmic, vision, and language datasets. Through extensive experiments, we demonstrate that models trained with harmonic loss outperform standard models by: (a) enhancing interpretability, (b) requiring less data for generalization, and (c) reducing grokking. Moreover, we compare a GPT-2 model trained with harmonic loss to the standard GPT-2, illustrating that the harmonic model develops more interpretable representations. Looking forward, we believe harmonic loss has the potential to become a valuable tool in domains with limited data availability or in high-stakes applications where interpretability and reliability are paramount, paving the way for more robust and efficient neural network models.

Generalization from Starvation: Hints of Universality in LLM Knowledge Graph Learning

Motivated by interpretability and reliability, we investigate how neural networks represent knowledge during graph learning, We find hints of universality, where equivalent representations are learned across a range of model sizes (from $10^2$ to $10^9$ parameters) and contexts (MLP toy models, LLM in-context learning and LLM training). We show that these attractor representations optimize generalization to unseen examples by exploiting properties of knowledge graph relations (e.g. symmetry and meta-transitivity). We find experimental support for such universality by showing that LLMs and simpler neural networks can be stitched, i.e., by stitching the first part of one model to the last part of another, mediated only by an affine or almost affine transformation. We hypothesize that this dynamic toward simplicity and generalization is driven by "intelligence from starvation": where overfitting is minimized by pressure to minimize the use of resources that are either scarce or competed for against other tasks.

GenEFT: Understanding Statics and Dynamics of Model Generalization via Effective Theory

We present GenEFT: an effective theory framework for shedding light on the statics and dynamics of neural network generalization, and illustrate it with graph learning examples. We first investigate the generalization phase transition as data size increases, comparing experimental results with information-theory-based approximations. We find generalization in a Goldilocks zone where the decoder is neither too weak nor too powerful. We then introduce an effective theory for the dynamics of representation learning, where latent-space representations are modeled as interacting particles (repons), and find that it explains our experimentally observed phase transition between generalization and overfitting as encoder and decoder learning rates are scanned. This highlights the power of physics-inspired effective theories for bridging the gap between theoretical predictions and practice in machine learning.