Scaling Laws For Scalable Oversight

Scalable oversight, the process by which weaker AI systems supervise stronger ones, has been proposed as a key strategy to control future superintelligent systems. However, it is still unclear how scalable oversight itself scales. To address this gap, we propose a framework that quantifies the probability of successful oversight as a function of the capabilities of the overseer and the system being overseen. Specifically, our framework models oversight as a game between capability-mismatched players; the players have oversight-specific and deception-specific Elo scores that are a piecewise-linear function of their general intelligence, with two plateaus corresponding to task incompetence and task saturation. We validate our framework with a modified version of the game Nim and then apply it to four oversight games: "Mafia", "Debate", "Backdoor Code" and "Wargames". For each game, we find scaling laws that approximate how domain performance depends on general AI system capability (using Chatbot Arena Elo as a proxy for general capability). We then build on our findings in a theoretical study of Nested Scalable Oversight (NSO), a process in which trusted models oversee untrusted stronger models, which then become the trusted models in the next step. We identify conditions under which NSO succeeds and derive numerically (and in some cases analytically) the optimal number of oversight levels to maximize the probability of oversight success. In our numerical examples, the NSO success rate is below 52% when overseeing systems that are 400 Elo points stronger than the baseline overseer, and it declines further for overseeing even stronger systems.

Are Sparse Autoencoders Useful? A Case Study in Sparse Probing

Sparse autoencoders (SAEs) are a popular method for interpreting concepts represented in large language model (LLM) activations. However, there is a lack of evidence regarding the validity of their interpretations due to the lack of a ground truth for the concepts used by an LLM, and a growing number of works have presented problems with current SAEs. One alternative source of evidence would be demonstrating that SAEs improve performance on downstream tasks beyond existing baselines. We test this by applying SAEs to the real-world task of LLM activation probing in four regimes: data scarcity, class imbalance, label noise, and covariate shift. Due to the difficulty of detecting concepts in these challenging settings, we hypothesize that SAEs' basis of interpretable, concept-level latents should provide a useful inductive bias. However, although SAEs occasionally perform better than baselines on individual datasets, we are unable to design ensemble methods combining SAEs with baselines that consistently outperform ensemble methods solely using baselines. Additionally, although SAEs initially appear promising for identifying spurious correlations, detecting poor dataset quality, and training multi-token probes, we are able to achieve similar results with simple non-SAE baselines as well. Though we cannot discount SAEs' utility on other tasks, our findings highlight the shortcomings of current SAEs and the need to rigorously evaluate interpretability methods on downstream tasks with strong baselines.

Language Models Use Trigonometry to Do Addition

Mathematical reasoning is an increasingly important indicator of large language model (LLM) capabilities, yet we lack understanding of how LLMs process even simple mathematical tasks. To address this, we reverse engineer how three mid-sized LLMs compute addition. We first discover that numbers are represented in these LLMs as a generalized helix, which is strongly causally implicated for the tasks of addition and subtraction, and is also causally relevant for integer division, multiplication, and modular arithmetic. We then propose that LLMs compute addition by manipulating this generalized helix using the "Clock" algorithm: to solve $a+b$, the helices for $a$ and $b$ are manipulated to produce the $a+b$ answer helix which is then read out to model logits. We model influential MLP outputs, attention head outputs, and even individual neuron preactivations with these helices and verify our understanding with causal interventions. By demonstrating that LLMs represent numbers on a helix and manipulate this helix to perform addition, we present the first representation-level explanation of an LLM's mathematical capability.

How Do Transformers "Do" Physics? Investigating the Simple Harmonic Oscillator

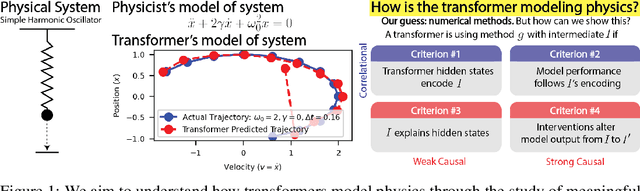
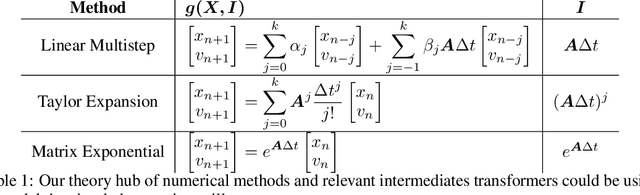
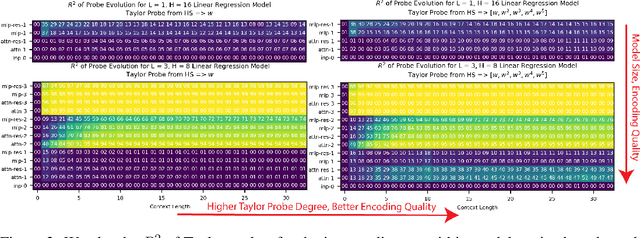
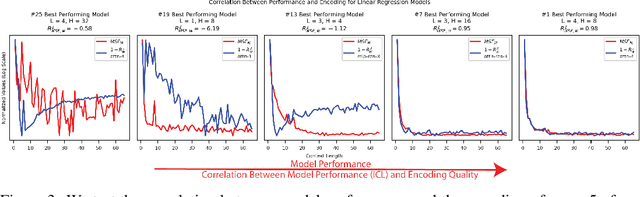
How do transformers model physics? Do transformers model systems with interpretable analytical solutions, or do they create "alien physics" that are difficult for humans to decipher? We take a step in demystifying this larger puzzle by investigating the simple harmonic oscillator (SHO), $\ddot{x}+2\gamma \dot{x}+\omega_0^2x=0$, one of the most fundamental systems in physics. Our goal is to identify the methods transformers use to model the SHO, and to do so we hypothesize and evaluate possible methods by analyzing the encoding of these methods' intermediates. We develop four criteria for the use of a method within the simple testbed of linear regression, where our method is $y = wx$ and our intermediate is $w$: (1) Can the intermediate be predicted from hidden states? (2) Is the intermediate's encoding quality correlated with model performance? (3) Can the majority of variance in hidden states be explained by the intermediate? (4) Can we intervene on hidden states to produce predictable outcomes? Armed with these two correlational (1,2), weak causal (3) and strong causal (4) criteria, we determine that transformers use known numerical methods to model trajectories of the simple harmonic oscillator, specifically the matrix exponential method. Our analysis framework can conveniently extend to high-dimensional linear systems and nonlinear systems, which we hope will help reveal the "world model" hidden in transformers.

OptPDE: Discovering Novel Integrable Systems via AI-Human Collaboration

Integrable partial differential equation (PDE) systems are of great interest in natural science, but are exceedingly rare and difficult to discover. To solve this, we introduce OptPDE, a first-of-its-kind machine learning approach that Optimizes PDEs' coefficients to maximize their number of conserved quantities, $n_{\rm CQ}$, and thus discover new integrable systems. We discover four families of integrable PDEs, one of which was previously known, and three of which have at least one conserved quantity but are new to the literature to the best of our knowledge. We investigate more deeply the properties of one of these novel PDE families, $u_t = (u_x+a^2u_{xxx})^3$. Our paper offers a promising schema of AI-human collaboration for integrable system discovery: machine learning generates interpretable hypotheses for possible integrable systems, which human scientists can verify and analyze, to truly close the discovery loop.

NuCLR: Nuclear Co-Learned Representations

We introduce Nuclear Co-Learned Representations (NuCLR), a deep learning model that predicts various nuclear observables, including binding and decay energies, and nuclear charge radii. The model is trained using a multi-task approach with shared representations and obtains state-of-the-art performance, achieving levels of precision that are crucial for understanding fundamental phenomena in nuclear (astro)physics. We also report an intriguing finding that the learned representation of NuCLR exhibits the prominent emergence of crucial aspects of the nuclear shell model, namely the shell structure, including the well-known magic numbers, and the Pauli Exclusion Principle. This suggests that the model is capable of capturing the underlying physical principles and that our approach has the potential to offer valuable insights into nuclear theory.