Transformers Can Navigate Mazes With Multi-Step Prediction

Despite their remarkable success in language modeling, transformers trained to predict the next token in a sequence struggle with long-term planning. This limitation is particularly evident in tasks requiring foresight to plan multiple steps ahead such as maze navigation. The standard next single token prediction objective, however, offers no explicit mechanism to predict multiple steps ahead - or revisit the path taken so far. Consequently, in this work we study whether explicitly predicting multiple steps ahead (and backwards) can improve transformers' maze navigation. We train parameter-matched transformers from scratch, under identical settings, to navigate mazes of varying types and sizes with standard next token prediction and MLM-U, an objective explicitly predicting multiple steps ahead and backwards. We find that MLM-U considerably improves transformers' ability to navigate mazes compared to standard next token prediction across maze types and complexities. We also find MLM-U training is 4x more sample efficient and converges 2x faster in terms of GPU training hours relative to next token training. Finally, for more complex mazes we find MLM-U benefits from scaling to larger transformers. Remarkably, we find transformers trained with MLM-U outperform larger transformers trained with next token prediction using additional supervision from A* search traces. We hope these findings underscore the promise of learning objectives to advance transformers' capacity for long-term planning.

The Factorization Curse: Which Tokens You Predict Underlie the Reversal Curse and More

Today's best language models still struggle with hallucinations: factually incorrect generations, which impede their ability to reliably retrieve information seen during training. The reversal curse, where models cannot recall information when probed in a different order than was encountered during training, exemplifies this in information retrieval. We reframe the reversal curse as a factorization curse - a failure of models to learn the same joint distribution under different factorizations. Through a series of controlled experiments with increasing levels of realism including WikiReversal, a setting we introduce to closely simulate a knowledge intensive finetuning task, we find that the factorization curse is an inherent failure of the next-token prediction objective used in popular large language models. Moreover, we demonstrate reliable information retrieval cannot be solved with scale, reversed tokens, or even naive bidirectional-attention training. Consequently, various approaches to finetuning on specialized data would necessarily provide mixed results on downstream tasks, unless the model has already seen the right sequence of tokens. Across five tasks of varying levels of complexity, our results uncover a promising path forward: factorization-agnostic objectives can significantly mitigate the reversal curse and hint at improved knowledge storage and planning capabilities.

From Neurons to Neutrons: A Case Study in Interpretability

Mechanistic Interpretability (MI) promises a path toward fully understanding how neural networks make their predictions. Prior work demonstrates that even when trained to perform simple arithmetic, models can implement a variety of algorithms (sometimes concurrently) depending on initialization and hyperparameters. Does this mean neuron-level interpretability techniques have limited applicability? We argue that high-dimensional neural networks can learn low-dimensional representations of their training data that are useful beyond simply making good predictions. Such representations can be understood through the mechanistic interpretability lens and provide insights that are surprisingly faithful to human-derived domain knowledge. This indicates that such approaches to interpretability can be useful for deriving a new understanding of a problem from models trained to solve it. As a case study, we extract nuclear physics concepts by studying models trained to reproduce nuclear data.

KBFormer: A Diffusion Model for Structured Entity Completion

We develop a generative attention-based approach to modeling structured entities comprising different property types, such as numerical, categorical, string, and composite. This approach handles such heterogeneous data through a mixed continuous-discrete diffusion process over the properties. Our flexible framework can model entities with arbitrary hierarchical properties, enabling applications to structured Knowledge Base (KB) entities and tabular data. Our approach obtains state-of-the-art performance on a majority of cases across 15 datasets. In addition, experiments with a device KB and a nuclear physics dataset demonstrate the model's ability to learn representations useful for entity completion in diverse settings. This has many downstream use cases, including modeling numerical properties with high accuracy - critical for science applications, which also benefit from the model's inherent probabilistic nature.

Expressive Monotonic Neural Networks

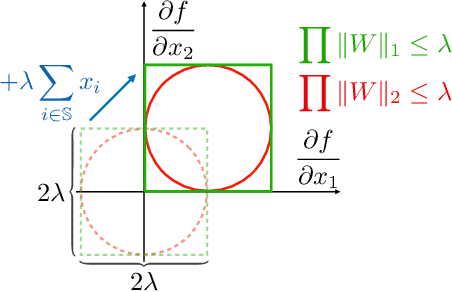
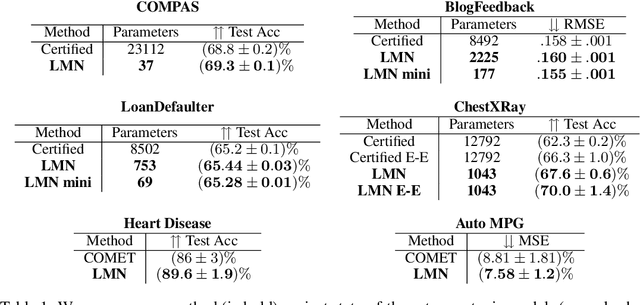
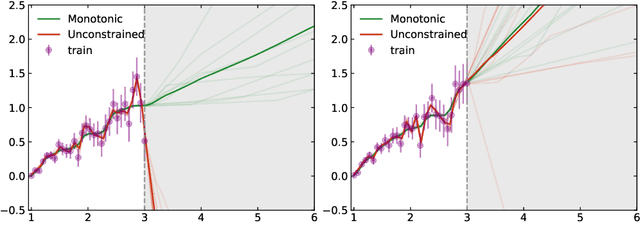
The monotonic dependence of the outputs of a neural network on some of its inputs is a crucial inductive bias in many scenarios where domain knowledge dictates such behavior. This is especially important for interpretability and fairness considerations. In a broader context, scenarios in which monotonicity is important can be found in finance, medicine, physics, and other disciplines. It is thus desirable to build neural network architectures that implement this inductive bias provably. In this work, we propose a weight-constrained architecture with a single residual connection to achieve exact monotonic dependence in any subset of the inputs. The weight constraint scheme directly controls the Lipschitz constant of the neural network and thus provides the additional benefit of robustness. Compared to currently existing techniques used for monotonicity, our method is simpler in implementation and in theory foundations, has negligible computational overhead, is guaranteed to produce monotonic dependence, and is highly expressive. We show how the algorithm is used to train powerful, robust, and interpretable discriminators that achieve competitive performance compared to current state-of-the-art methods across various benchmarks, from social applications to the classification of the decays of subatomic particles produced at the CERN Large Hadron Collider.

NuCLR: Nuclear Co-Learned Representations

We introduce Nuclear Co-Learned Representations (NuCLR), a deep learning model that predicts various nuclear observables, including binding and decay energies, and nuclear charge radii. The model is trained using a multi-task approach with shared representations and obtains state-of-the-art performance, achieving levels of precision that are crucial for understanding fundamental phenomena in nuclear (astro)physics. We also report an intriguing finding that the learned representation of NuCLR exhibits the prominent emergence of crucial aspects of the nuclear shell model, namely the shell structure, including the well-known magic numbers, and the Pauli Exclusion Principle. This suggests that the model is capable of capturing the underlying physical principles and that our approach has the potential to offer valuable insights into nuclear theory.

Finding NEEMo: Geometric Fitting using Neural Estimation of the Energy Mover's Distance

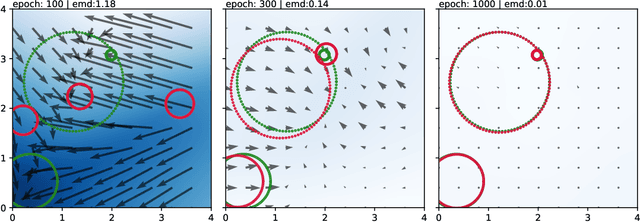
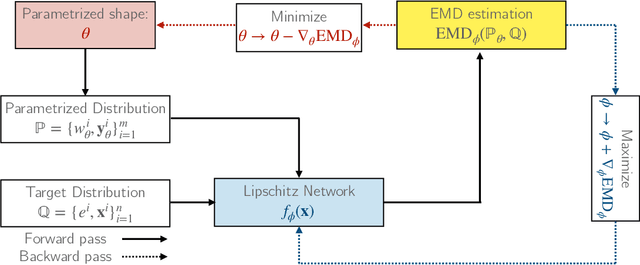
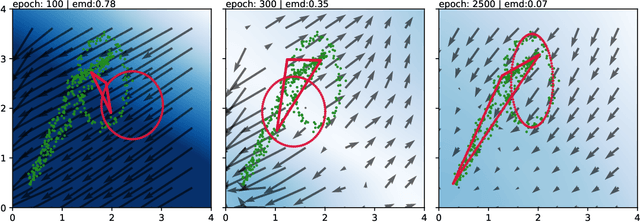
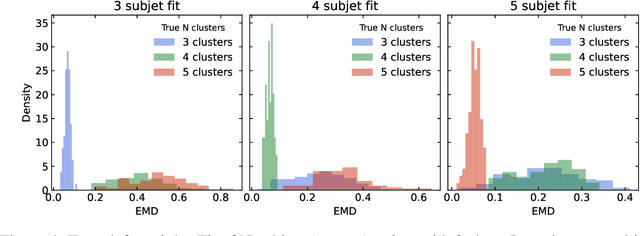
A novel neural architecture was recently developed that enforces an exact upper bound on the Lipschitz constant of the model by constraining the norm of its weights in a minimal way, resulting in higher expressiveness compared to other techniques. We present a new and interesting direction for this architecture: estimation of the Wasserstein metric (Earth Mover's Distance) in optimal transport by employing the Kantorovich-Rubinstein duality to enable its use in geometric fitting applications. Specifically, we focus on the field of high-energy particle physics, where it has been shown that a metric for the space of particle-collider events can be defined based on the Wasserstein metric, referred to as the Energy Mover's Distance (EMD). This metrization has the potential to revolutionize data-driven collider phenomenology. The work presented here represents a major step towards realizing this goal by providing a differentiable way of directly calculating the EMD. We show how the flexibility that our approach enables can be used to develop novel clustering algorithms.

Towards Understanding Grokking: An Effective Theory of Representation Learning

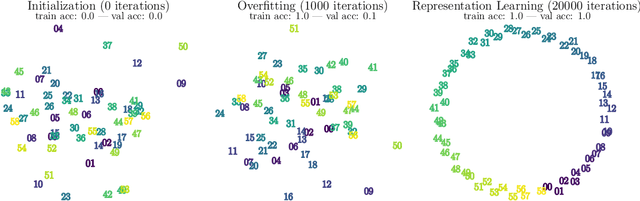
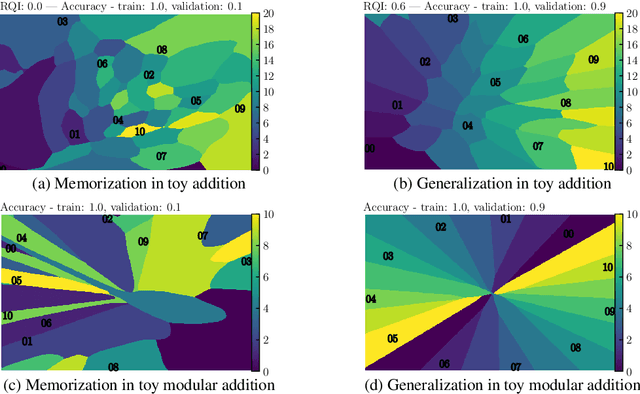
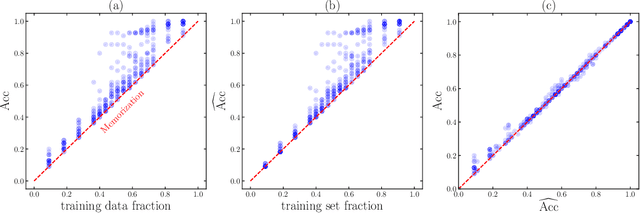
We aim to understand grokking, a phenomenon where models generalize long after overfitting their training set. We present both a microscopic analysis anchored by an effective theory and a macroscopic analysis of phase diagrams describing learning performance across hyperparameters. We find that generalization originates from structured representations whose training dynamics and dependence on training set size can be predicted by our effective theory in a toy setting. We observe empirically the presence of four learning phases: comprehension, grokking, memorization, and confusion. We find representation learning to occur only in a "Goldilocks zone" (including comprehension and grokking) between memorization and confusion. Compared to the comprehension phase, the grokking phase stays closer to the memorization phase, leading to delayed generalization. The Goldilocks phase is reminiscent of "intelligence from starvation" in Darwinian evolution, where resource limitations drive discovery of more efficient solutions. This study not only provides intuitive explanations of the origin of grokking, but also highlights the usefulness of physics-inspired tools, e.g., effective theories and phase diagrams, for understanding deep learning.

Robust and Provably Monotonic Networks

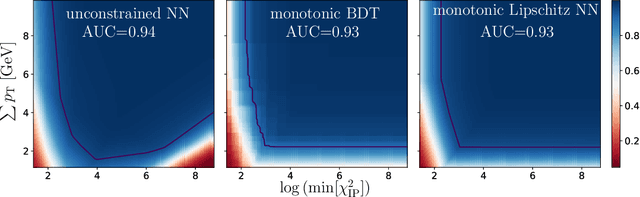
The Lipschitz constant of the map between the input and output space represented by a neural network is a natural metric for assessing the robustness of the model. We present a new method to constrain the Lipschitz constant of dense deep learning models that can also be generalized to other architectures. The method relies on a simple weight normalization scheme during training that ensures the Lipschitz constant of every layer is below an upper limit specified by the analyst. A simple residual connection can then be used to make the model monotonic in any subset of its inputs, which is useful in scenarios where domain knowledge dictates such dependence. Examples can be found in algorithmic fairness requirements or, as presented here, in the classification of the decays of subatomic particles produced at the CERN Large Hadron Collider. Our normalization is minimally constraining and allows the underlying architecture to maintain higher expressiveness compared to other techniques which aim to either control the Lipschitz constant of the model or ensure its monotonicity. We show how the algorithm was used to train a powerful, robust, and interpretable discriminator for heavy-flavor decays in the LHCb realtime data-processing system.