Finding NEEMo: Geometric Fitting using Neural Estimation of the Energy Mover's Distance
Paper and Code
Sep 30, 2022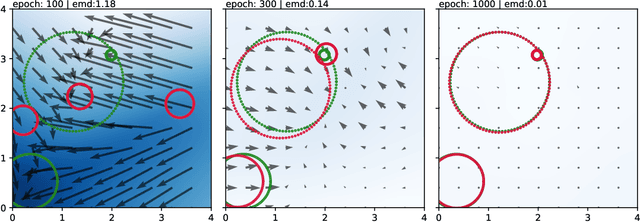
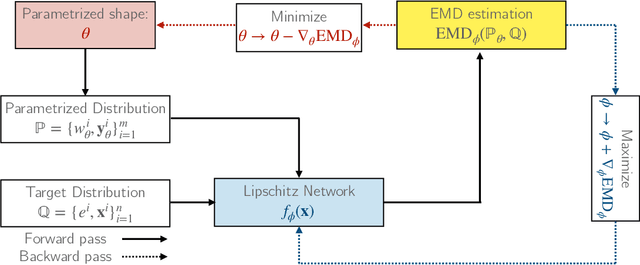
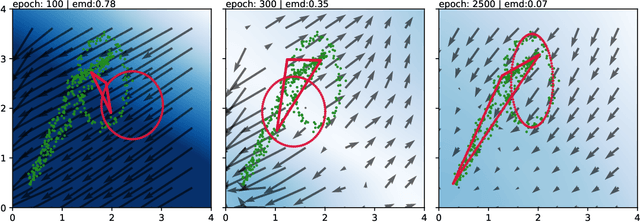
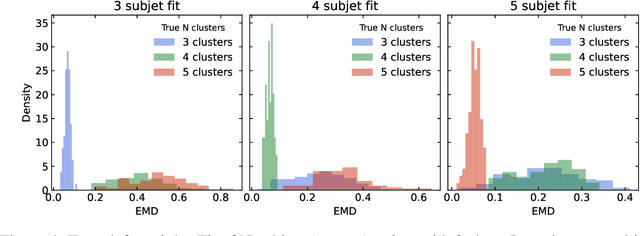
A novel neural architecture was recently developed that enforces an exact upper bound on the Lipschitz constant of the model by constraining the norm of its weights in a minimal way, resulting in higher expressiveness compared to other techniques. We present a new and interesting direction for this architecture: estimation of the Wasserstein metric (Earth Mover's Distance) in optimal transport by employing the Kantorovich-Rubinstein duality to enable its use in geometric fitting applications. Specifically, we focus on the field of high-energy particle physics, where it has been shown that a metric for the space of particle-collider events can be defined based on the Wasserstein metric, referred to as the Energy Mover's Distance (EMD). This metrization has the potential to revolutionize data-driven collider phenomenology. The work presented here represents a major step towards realizing this goal by providing a differentiable way of directly calculating the EMD. We show how the flexibility that our approach enables can be used to develop novel clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge