From Neurons to Neutrons: A Case Study in Interpretability

Mechanistic Interpretability (MI) promises a path toward fully understanding how neural networks make their predictions. Prior work demonstrates that even when trained to perform simple arithmetic, models can implement a variety of algorithms (sometimes concurrently) depending on initialization and hyperparameters. Does this mean neuron-level interpretability techniques have limited applicability? We argue that high-dimensional neural networks can learn low-dimensional representations of their training data that are useful beyond simply making good predictions. Such representations can be understood through the mechanistic interpretability lens and provide insights that are surprisingly faithful to human-derived domain knowledge. This indicates that such approaches to interpretability can be useful for deriving a new understanding of a problem from models trained to solve it. As a case study, we extract nuclear physics concepts by studying models trained to reproduce nuclear data.

NuCLR: Nuclear Co-Learned Representations

We introduce Nuclear Co-Learned Representations (NuCLR), a deep learning model that predicts various nuclear observables, including binding and decay energies, and nuclear charge radii. The model is trained using a multi-task approach with shared representations and obtains state-of-the-art performance, achieving levels of precision that are crucial for understanding fundamental phenomena in nuclear (astro)physics. We also report an intriguing finding that the learned representation of NuCLR exhibits the prominent emergence of crucial aspects of the nuclear shell model, namely the shell structure, including the well-known magic numbers, and the Pauli Exclusion Principle. This suggests that the model is capable of capturing the underlying physical principles and that our approach has the potential to offer valuable insights into nuclear theory.

Finding NEEMo: Geometric Fitting using Neural Estimation of the Energy Mover's Distance

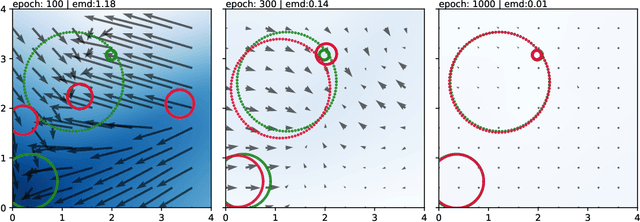
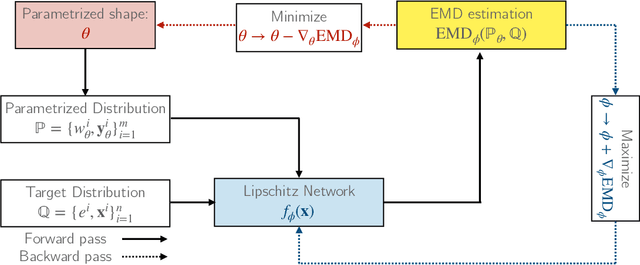
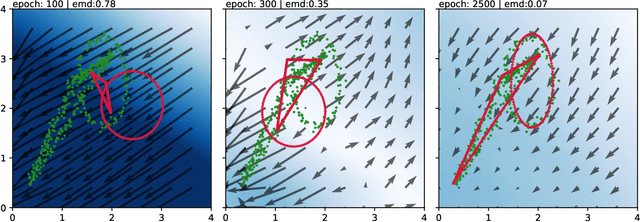
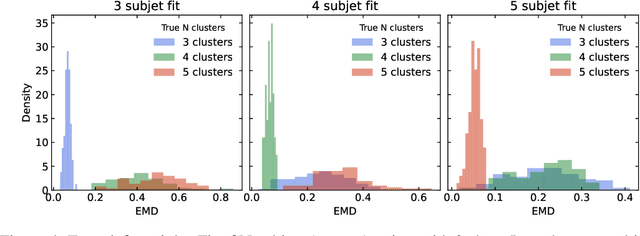
A novel neural architecture was recently developed that enforces an exact upper bound on the Lipschitz constant of the model by constraining the norm of its weights in a minimal way, resulting in higher expressiveness compared to other techniques. We present a new and interesting direction for this architecture: estimation of the Wasserstein metric (Earth Mover's Distance) in optimal transport by employing the Kantorovich-Rubinstein duality to enable its use in geometric fitting applications. Specifically, we focus on the field of high-energy particle physics, where it has been shown that a metric for the space of particle-collider events can be defined based on the Wasserstein metric, referred to as the Energy Mover's Distance (EMD). This metrization has the potential to revolutionize data-driven collider phenomenology. The work presented here represents a major step towards realizing this goal by providing a differentiable way of directly calculating the EMD. We show how the flexibility that our approach enables can be used to develop novel clustering algorithms.

Towards Understanding Grokking: An Effective Theory of Representation Learning

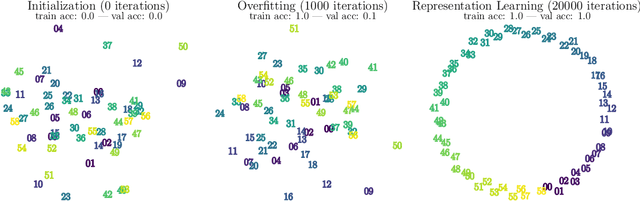
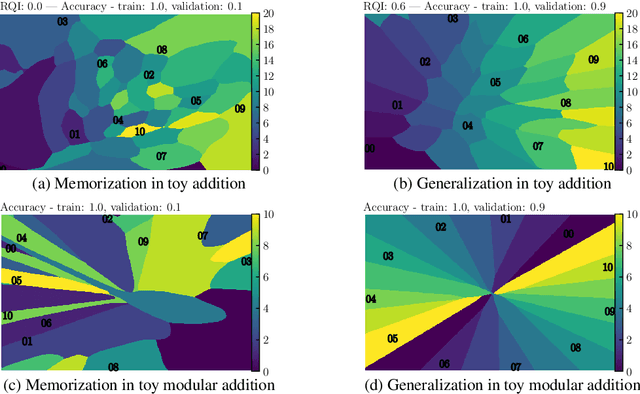
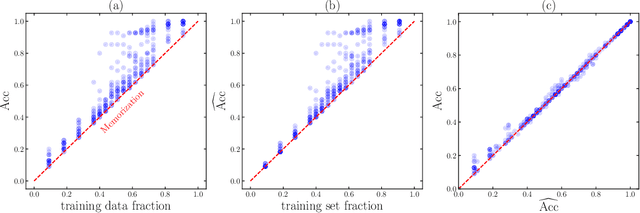
We aim to understand grokking, a phenomenon where models generalize long after overfitting their training set. We present both a microscopic analysis anchored by an effective theory and a macroscopic analysis of phase diagrams describing learning performance across hyperparameters. We find that generalization originates from structured representations whose training dynamics and dependence on training set size can be predicted by our effective theory in a toy setting. We observe empirically the presence of four learning phases: comprehension, grokking, memorization, and confusion. We find representation learning to occur only in a "Goldilocks zone" (including comprehension and grokking) between memorization and confusion. Compared to the comprehension phase, the grokking phase stays closer to the memorization phase, leading to delayed generalization. The Goldilocks phase is reminiscent of "intelligence from starvation" in Darwinian evolution, where resource limitations drive discovery of more efficient solutions. This study not only provides intuitive explanations of the origin of grokking, but also highlights the usefulness of physics-inspired tools, e.g., effective theories and phase diagrams, for understanding deep learning.

Robust and Provably Monotonic Networks

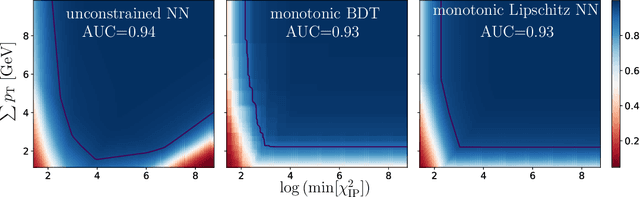
The Lipschitz constant of the map between the input and output space represented by a neural network is a natural metric for assessing the robustness of the model. We present a new method to constrain the Lipschitz constant of dense deep learning models that can also be generalized to other architectures. The method relies on a simple weight normalization scheme during training that ensures the Lipschitz constant of every layer is below an upper limit specified by the analyst. A simple residual connection can then be used to make the model monotonic in any subset of its inputs, which is useful in scenarios where domain knowledge dictates such dependence. Examples can be found in algorithmic fairness requirements or, as presented here, in the classification of the decays of subatomic particles produced at the CERN Large Hadron Collider. Our normalization is minimally constraining and allows the underlying architecture to maintain higher expressiveness compared to other techniques which aim to either control the Lipschitz constant of the model or ensure its monotonicity. We show how the algorithm was used to train a powerful, robust, and interpretable discriminator for heavy-flavor decays in the LHCb realtime data-processing system.