FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

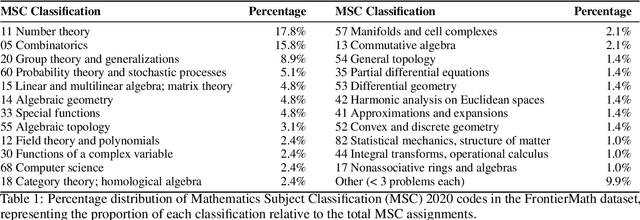
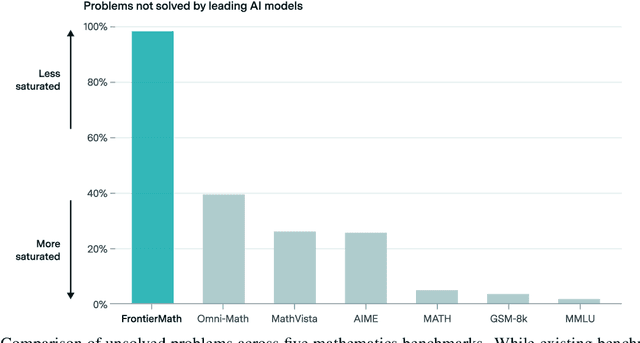
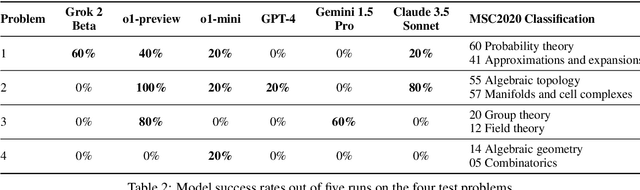
We introduce FrontierMath, a benchmark of hundreds of original, exceptionally challenging mathematics problems crafted and vetted by expert mathematicians. The questions cover most major branches of modern mathematics -- from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. Solving a typical problem requires multiple hours of effort from a researcher in the relevant branch of mathematics, and for the upper end questions, multiple days. FrontierMath uses new, unpublished problems and automated verification to reliably evaluate models while minimizing risk of data contamination. Current state-of-the-art AI models solve under 2% of problems, revealing a vast gap between AI capabilities and the prowess of the mathematical community. As AI systems advance toward expert-level mathematical abilities, FrontierMath offers a rigorous testbed that quantifies their progress.

Explaining Bayesian Networks in Natural Language using Factor Arguments. Evaluation in the medical domain

In this paper, we propose a model for building natural language explanations for Bayesian Network Reasoning in terms of factor arguments, which are argumentation graphs of flowing evidence, relating the observed evidence to a target variable we want to learn about. We introduce the notion of factor argument independence to address the outstanding question of defining when arguments should be presented jointly or separately and present an algorithm that, starting from the evidence nodes and a target node, produces a list of all independent factor arguments ordered by their strength. Finally, we implemented a scheme to build natural language explanations of Bayesian Reasoning using this approach. Our proposal has been validated in the medical domain through a human-driven evaluation study where we compare the Bayesian Network Reasoning explanations obtained using factor arguments with an alternative explanation method. Evaluation results indicate that our proposed explanation approach is deemed by users as significantly more useful for understanding Bayesian Network Reasoning than another existing explanation method it is compared to.

Algorithmic progress in language models

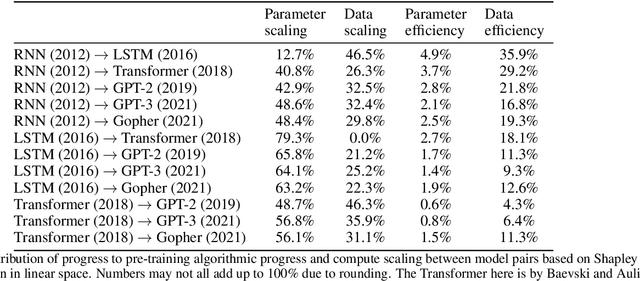
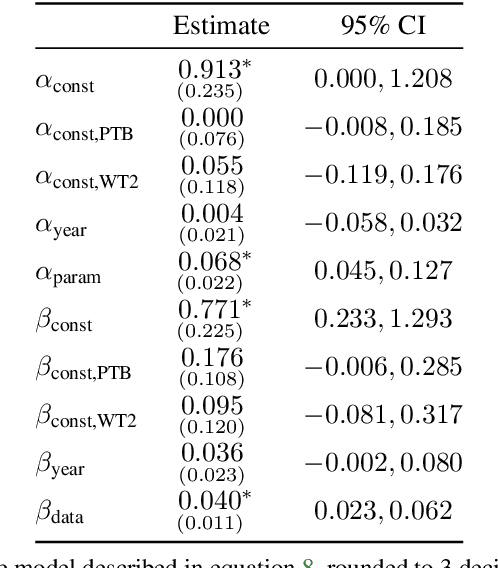
We investigate the rate at which algorithms for pre-training language models have improved since the advent of deep learning. Using a dataset of over 200 language model evaluations on Wikitext and Penn Treebank spanning 2012-2023, we find that the compute required to reach a set performance threshold has halved approximately every 8 months, with a 95% confidence interval of around 5 to 14 months, substantially faster than hardware gains per Moore's Law. We estimate augmented scaling laws, which enable us to quantify algorithmic progress and determine the relative contributions of scaling models versus innovations in training algorithms. Despite the rapid pace of algorithmic progress and the development of new architectures such as the transformer, our analysis reveals that the increase in compute made an even larger contribution to overall performance improvements over this time period. Though limited by noisy benchmark data, our analysis quantifies the rapid progress in language modeling, shedding light on the relative contributions from compute and algorithms.

Power Law Trends in Speedrunning and Machine Learning

We find that improvements in speedrunning world records follow a power law pattern. Using this observation, we answer an outstanding question from previous work: How do we improve on the baseline of predicting no improvement when forecasting speedrunning world records out to some time horizon, such as one month? Using a random effects model, we improve on this baseline for relative mean square error made on predicting out-of-sample world record improvements as the comparison metric at a $p < 10^{-5}$ significance level. The same set-up improves \textit{even} on the ex-post best exponential moving average forecasts at a $p = 0.15$ significance level while having access to substantially fewer data points. We demonstrate the effectiveness of this approach by applying it to Machine Learning benchmarks and achieving forecasts that exceed a baseline. Finally, we interpret the resulting model to suggest that 1) ML benchmarks are far from saturation and 2) sudden large improvements in Machine Learning are unlikely but cannot be ruled out.

Machine Learning Model Sizes and the Parameter Gap

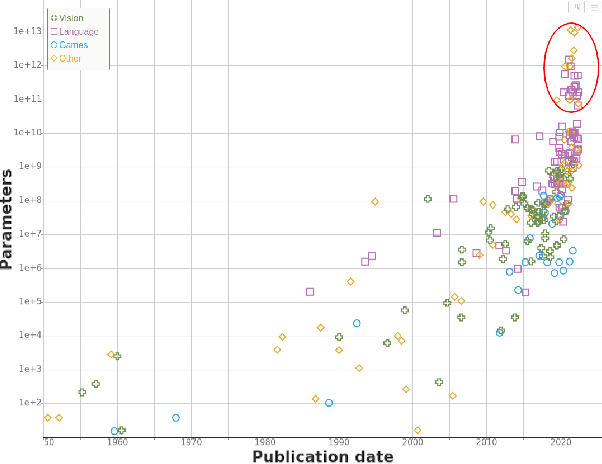
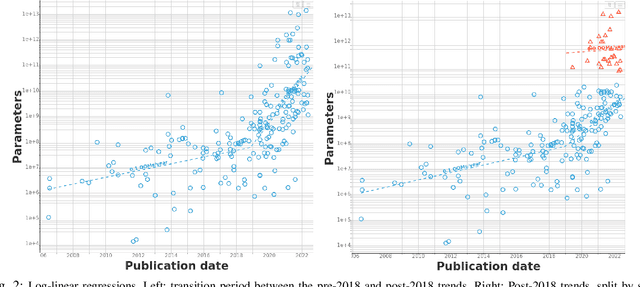
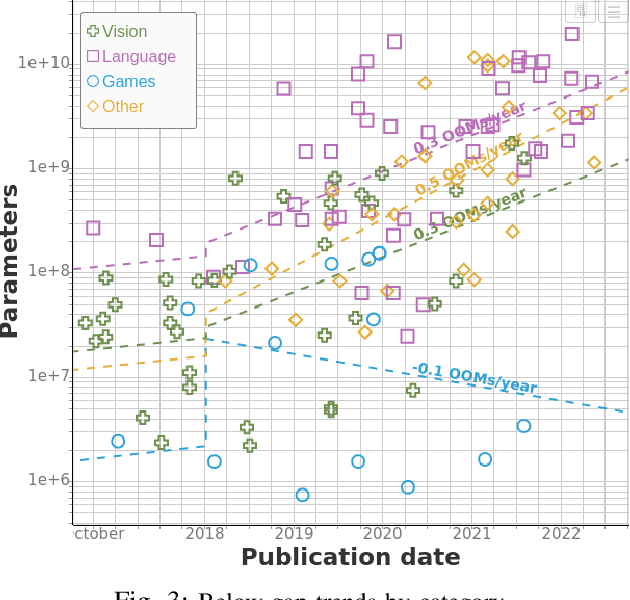
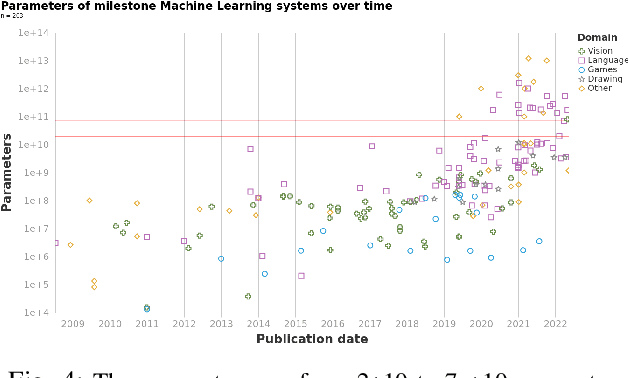
We study trends in model size of notable machine learning systems over time using a curated dataset. From 1950 to 2018, model size in language models increased steadily by seven orders of magnitude. The trend then accelerated, with model size increasing by another five orders of magnitude in just 4 years from 2018 to 2022. Vision models grew at a more constant pace, totaling 7 orders of magnitude of growth between 1950 and 2022. We also identify that, since 2020, there have been many language models below 20B parameters, many models above 70B parameters, but a scarcity of models in the 20-70B parameter range. We refer to that scarcity as the parameter gap. We provide some stylized facts about the parameter gap and propose a few hypotheses to explain it. The explanations we favor are: (a) increasing model size beyond 20B parameters requires adopting different parallelism techniques, which makes mid-sized models less cost-effective, (b) GPT-3 was one order of magnitude larger than previous language models, and researchers afterwards primarily experimented with bigger models to outperform it. While these dynamics likely exist, and we believe they play some role in generating the gap, we don't have high confidence that there are no other, more important dynamics at play.

Compute Trends Across Three Eras of Machine Learning

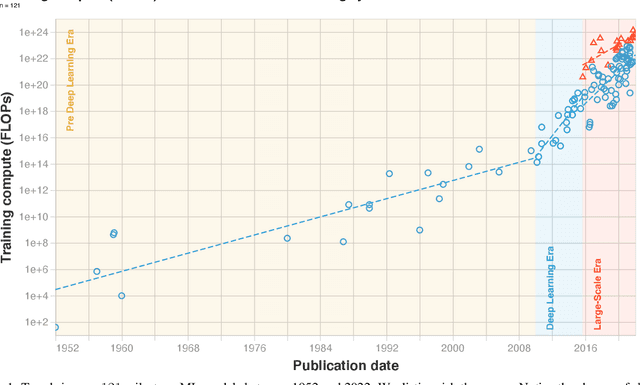
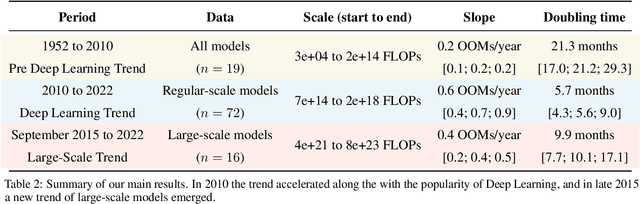
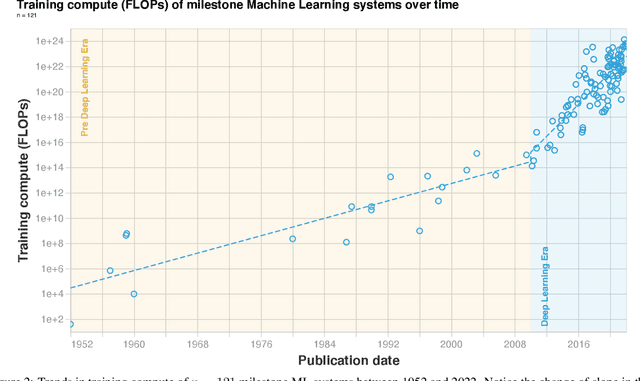
Compute, data, and algorithmic advances are the three fundamental factors that guide the progress of modern Machine Learning (ML). In this paper we study trends in the most readily quantified factor - compute. We show that before 2010 training compute grew in line with Moore's law, doubling roughly every 20 months. Since the advent of Deep Learning in the early 2010s, the scaling of training compute has accelerated, doubling approximately every 6 months. In late 2015, a new trend emerged as firms developed large-scale ML models with 10 to 100-fold larger requirements in training compute. Based on these observations we split the history of compute in ML into three eras: the Pre Deep Learning Era, the Deep Learning Era and the Large-Scale Era. Overall, our work highlights the fast-growing compute requirements for training advanced ML systems.

Finding, Scoring and Explaining Arguments in Bayesian Networks

We propose a new approach to explain Bayesian Networks. The approach revolves around a new definition of a probabilistic argument and the evidence it provides. We define a notion of independent arguments, and propose an algorithm to extract a list of relevant, independent arguments given a Bayesian Network, a target node and a set of observations. To demonstrate the relevance of the arguments, we show how we can use the extracted arguments to approximate message passing. Finally, we show a simple scheme to explain the arguments in natural language.

Implications of Quantum Computing for Artificial Intelligence alignment research

We explain some key features of quantum computing via three heuristics and apply them to argue that a deep understanding of quantum computing is unlikely to be helpful to address current bottlenecks in Artificial Intelligence Alignment. Our argument relies on the claims that Quantum Computing leads to compute overhang instead of algorithmic overhang, and that the difficulties associated with the measurement of quantum states do not invalidate any major assumptions of current Artificial Intelligence Alignment research agendas. We also discuss tripwiring, adversarial blinding, informed oversight and side effects as possible exceptions.