FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

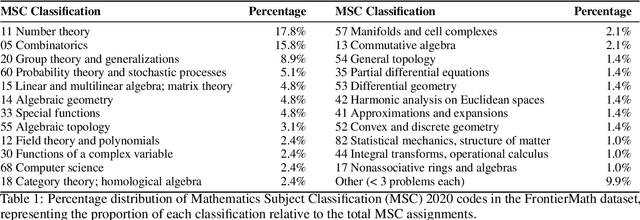
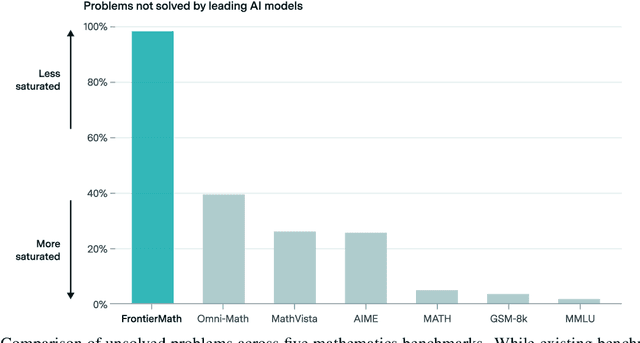
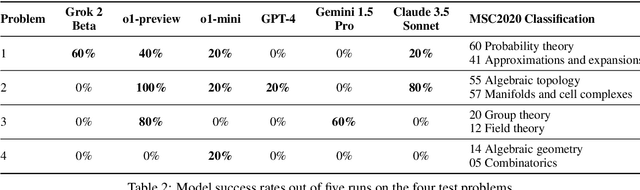
We introduce FrontierMath, a benchmark of hundreds of original, exceptionally challenging mathematics problems crafted and vetted by expert mathematicians. The questions cover most major branches of modern mathematics -- from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. Solving a typical problem requires multiple hours of effort from a researcher in the relevant branch of mathematics, and for the upper end questions, multiple days. FrontierMath uses new, unpublished problems and automated verification to reliably evaluate models while minimizing risk of data contamination. Current state-of-the-art AI models solve under 2% of problems, revealing a vast gap between AI capabilities and the prowess of the mathematical community. As AI systems advance toward expert-level mathematical abilities, FrontierMath offers a rigorous testbed that quantifies their progress.

An Empirical Study of Scaling Laws for Transfer

We present a limited empirical study of scaling laws for transfer learning in transformer models. More specifically, we examine a scaling law that incorporates a "transfer gap" term, indicating the effectiveness of pre-training on one distribution when optimizing for downstream performance on another distribution. When the transfer gap is low, pre-training is a cost-effective strategy for improving downstream performance. Conversely, when the gap is high, collecting high-quality fine-tuning data becomes relatively more cost effective. Fitting the scaling law to experiments from diverse datasets reveals significant variations in the transfer gap across distributions. In theory, the scaling law can inform optimal data allocation strategies and highlights how the scarcity of downstream data can bottleneck performance. Our findings contribute to a principled way to measure transfer learning efficiency and understand how data availability affects capabilities.

Chinchilla Scaling: A replication attempt

Hoffmann et al. (2022) propose three methods for estimating a compute-optimal scaling law. We attempt to replicate their third estimation procedure, which involves fitting a parametric loss function to a reconstruction of data from their plots. We find that the reported estimates are inconsistent with their first two estimation methods, fail at fitting the extracted data, and report implausibly narrow confidence intervals--intervals this narrow would require over 600,000 experiments, while they likely only ran fewer than 500. In contrast, our rederivation of the scaling law using the third approach yields results that are compatible with the findings from the first two estimation procedures described by Hoffmann et al.