Ex$^2$MCMC: Sampling through Exploration Exploitation
Paper and Code
Nov 04, 2021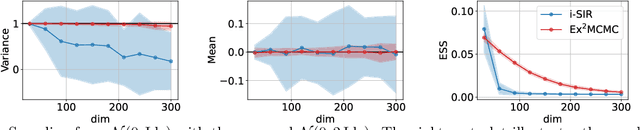
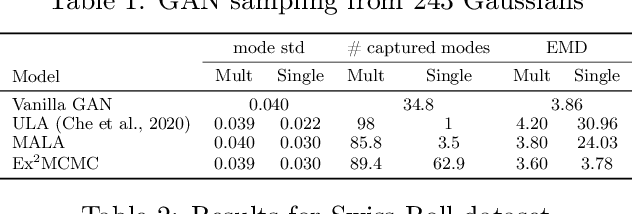
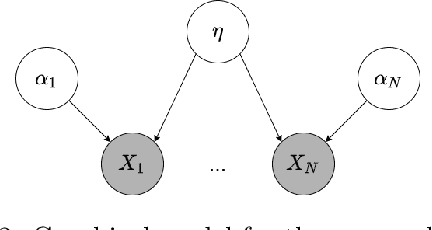
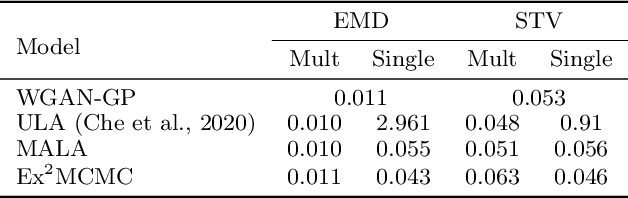
We develop an Explore-Exploit Markov chain Monte Carlo algorithm ($\operatorname{Ex^2MCMC}$) that combines multiple global proposals and local moves. The proposed method is massively parallelizable and extremely computationally efficient. We prove $V$-uniform geometric ergodicity of $\operatorname{Ex^2MCMC}$ under realistic conditions and compute explicit bounds on the mixing rate showing the improvement brought by the multiple global moves. We show that $\operatorname{Ex^2MCMC}$ allows fine-tuning of exploitation (local moves) and exploration (global moves) via a novel approach to proposing dependent global moves. Finally, we develop an adaptive scheme, $\operatorname{FlEx^2MCMC}$, that learns the distribution of global moves using normalizing flows. We illustrate the efficiency of $\operatorname{Ex^2MCMC}$ and its adaptive versions on many classical sampling benchmarks. We also show that these algorithms improve the quality of sampling GANs as energy-based models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge