Improved Central Limit Theorem and Bootstrap Approximations for Linear Stochastic Approximation

In this paper, we refine the Berry-Esseen bounds for the multivariate normal approximation of Polyak-Ruppert averaged iterates arising from the linear stochastic approximation (LSA) algorithm with decreasing step size. We consider the normal approximation by the Gaussian distribution with covariance matrix predicted by the Polyak-Juditsky central limit theorem and establish the rate up to order $n^{-1/3}$ in convex distance, where $n$ is the number of samples used in the algorithm. We also prove a non-asymptotic validity of the multiplier bootstrap procedure for approximating the distribution of the rescaled error of the averaged LSA estimator. We establish approximation rates of order up to $1/\sqrt{n}$ for the latter distribution, which significantly improves upon the previous results obtained by Samsonov et al. (2024).

On the Rate of Gaussian Approximation for Linear Regression Problems

In this paper, we consider the problem of Gaussian approximation for the online linear regression task. We derive the corresponding rates for the setting of a constant learning rate and study the explicit dependence of the convergence rate upon the problem dimension $d$ and quantities related to the design matrix. When the number of iterations $n$ is known in advance, our results yield the rate of normal approximation of order $\sqrt{\log{n}/n}$, provided that the sample size $n$ is large enough.

Gaussian Approximation for Two-Timescale Linear Stochastic Approximation

In this paper, we establish non-asymptotic bounds for accuracy of normal approximation for linear two-timescale stochastic approximation (TTSA) algorithms driven by martingale difference or Markov noise. Focusing on both the last iterate and Polyak-Ruppert averaging regimes, we derive bounds for normal approximation in terms of the convex distance between probability distributions. Our analysis reveals a non-trivial interaction between the fast and slow timescales: the normal approximation rate for the last iterate improves as the timescale separation increases, while it decreases in the Polyak-Ruppert averaged setting. We also provide the high-order moment bounds for the error of linear TTSA algorithm, which may be of independent interest.

High-Order Error Bounds for Markovian LSA with Richardson-Romberg Extrapolation

In this paper, we study the bias and high-order error bounds of the Linear Stochastic Approximation (LSA) algorithm with Polyak-Ruppert (PR) averaging under Markovian noise. We focus on the version of the algorithm with constant step size $\alpha$ and propose a novel decomposition of the bias via a linearization technique. We analyze the structure of the bias and show that the leading-order term is linear in $\alpha$ and cannot be eliminated by PR averaging. To address this, we apply the Richardson-Romberg (RR) extrapolation procedure, which effectively cancels the leading bias term. We derive high-order moment bounds for the RR iterates and show that the leading error term aligns with the asymptotically optimal covariance matrix of the vanilla averaged LSA iterates.

On the Upper Bounds for the Matrix Spectral Norm

We consider the problem of estimating the spectral norm of a matrix using only matrix-vector products. We propose a new Counterbalance estimator that provides upper bounds on the norm and derive probabilistic guarantees on its underestimation. Compared to standard approaches such as the power method, the proposed estimator produces significantly tighter upper bounds in both synthetic and real-world settings. Our method is especially effective for matrices with fast-decaying spectra, such as those arising in deep learning and inverse problems.

Statistical inference for Linear Stochastic Approximation with Markovian Noise

In this paper we derive non-asymptotic Berry-Esseen bounds for Polyak-Ruppert averaged iterates of the Linear Stochastic Approximation (LSA) algorithm driven by the Markovian noise. Our analysis yields $\mathcal{O}(n^{-1/4})$ convergence rates to the Gaussian limit in the Kolmogorov distance. We further establish the non-asymptotic validity of a multiplier block bootstrap procedure for constructing the confidence intervals, guaranteeing consistent inference under Markovian sampling. Our work provides the first non-asymptotic guarantees on the rate of convergence of bootstrap-based confidence intervals for stochastic approximation with Markov noise. Moreover, we recover the classical rate of order $\mathcal{O}(n^{-1/8})$ up to logarithmic factors for estimating the asymptotic variance of the iterates of the LSA algorithm.

A note on concentration inequalities for the overlapped batch mean variance estimators for Markov chains

In this paper, we study the concentration properties of quadratic forms associated with Markov chains using the martingale decomposition method introduced by Atchad\'e and Cattaneo (2014). In particular, we derive concentration inequalities for the overlapped batch mean (OBM) estimators of the asymptotic variance for uniformly geometrically ergodic Markov chains. Our main result provides an explicit control of the $p$-th moment of the difference between the OBM estimator and the asymptotic variance of the Markov chain with explicit dependence upon $p$ and mixing time of the underlying Markov chain.

Revisiting Non-Acyclic GFlowNets in Discrete Environments

Generative Flow Networks (GFlowNets) are a family of generative models that learn to sample objects from a given probability distribution, potentially known up to a normalizing constant. Instead of working in the object space, GFlowNets proceed by sampling trajectories in an appropriately constructed directed acyclic graph environment, greatly relying on the acyclicity of the graph. In our paper, we revisit the theory that relaxes the acyclicity assumption and present a simpler theoretical framework for non-acyclic GFlowNets in discrete environments. Moreover, we provide various novel theoretical insights related to training with fixed backward policies, the nature of flow functions, and connections between entropy-regularized RL and non-acyclic GFlowNets, which naturally generalize the respective concepts and theoretical results from the acyclic setting. In addition, we experimentally re-examine the concept of loss stability in non-acyclic GFlowNet training, as well as validate our own theoretical findings.

Refined Analysis of Federated Averaging's Bias and Federated Richardson-Romberg Extrapolation

In this paper, we present a novel analysis of FedAvg with constant step size, relying on the Markov property of the underlying process. We demonstrate that the global iterates of the algorithm converge to a stationary distribution and analyze its resulting bias and variance relative to the problem's solution. We provide a first-order expansion of the bias in both homogeneous and heterogeneous settings. Interestingly, this bias decomposes into two distinct components: one that depends solely on stochastic gradient noise and another on client heterogeneity. Finally, we introduce a new algorithm based on the Richardson-Romberg extrapolation technique to mitigate this bias.

Optimizing Backward Policies in GFlowNets via Trajectory Likelihood Maximization

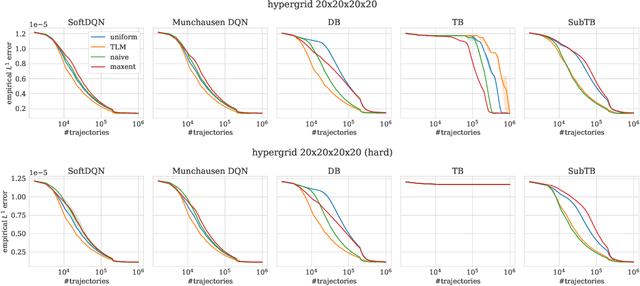
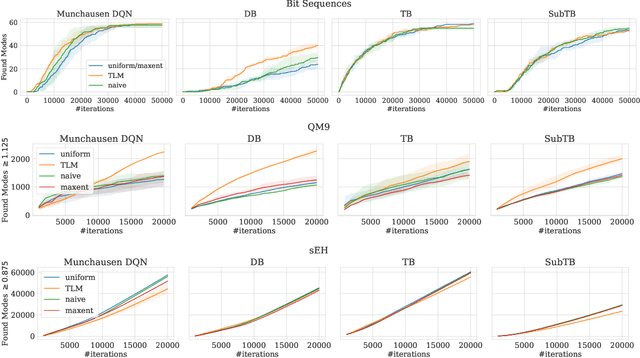
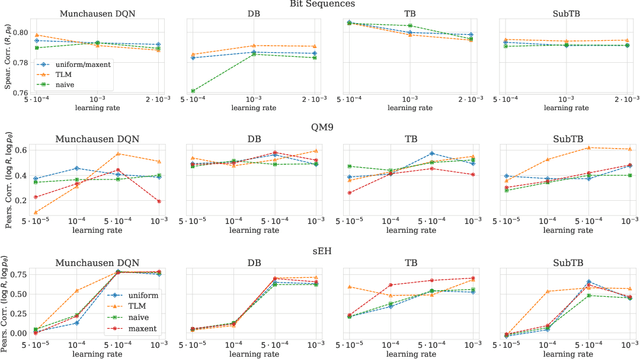
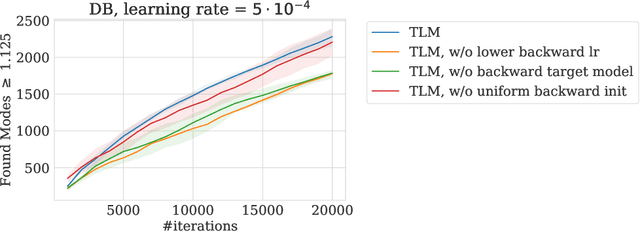
Generative Flow Networks (GFlowNets) are a family of generative models that learn to sample objects with probabilities proportional to a given reward function. The key concept behind GFlowNets is the use of two stochastic policies: a forward policy, which incrementally constructs compositional objects, and a backward policy, which sequentially deconstructs them. Recent results show a close relationship between GFlowNet training and entropy-regularized reinforcement learning (RL) problems with a particular reward design. However, this connection applies only in the setting of a fixed backward policy, which might be a significant limitation. As a remedy to this problem, we introduce a simple backward policy optimization algorithm that involves direct maximization of the value function in an entropy-regularized Markov Decision Process (MDP) over intermediate rewards. We provide an extensive experimental evaluation of the proposed approach across various benchmarks in combination with both RL and GFlowNet algorithms and demonstrate its faster convergence and mode discovery in complex environments.