Tight Bounds for Schrödinger Potential Estimation in Unpaired Image-to-Image Translation Problems

Modern methods of generative modelling and unpaired image-to-image translation based on Schr\"odinger bridges and stochastic optimal control theory aim to transform an initial density to a target one in an optimal way. In the present paper, we assume that we only have access to i.i.d. samples from initial and final distributions. This makes our setup suitable for both generative modelling and unpaired image-to-image translation. Relying on the stochastic optimal control approach, we choose an Ornstein-Uhlenbeck process as the reference one and estimate the corresponding Schr\"odinger potential. Introducing a risk function as the Kullback-Leibler divergence between couplings, we derive tight bounds on generalization ability of an empirical risk minimizer in a class of Schr\"odinger potentials including Gaussian mixtures. Thanks to the mixing properties of the Ornstein-Uhlenbeck process, we almost achieve fast rates of convergence up to some logarithmic factors in favourable scenarios. We also illustrate performance of the suggested approach with numerical experiments.

Accelerating Nash Learning from Human Feedback via Mirror Prox

Traditional Reinforcement Learning from Human Feedback (RLHF) often relies on reward models, frequently assuming preference structures like the Bradley-Terry model, which may not accurately capture the complexities of real human preferences (e.g., intransitivity). Nash Learning from Human Feedback (NLHF) offers a more direct alternative by framing the problem as finding a Nash equilibrium of a game defined by these preferences. In this work, we introduce Nash Mirror Prox ($\mathtt{Nash-MP}$), an online NLHF algorithm that leverages the Mirror Prox optimization scheme to achieve fast and stable convergence to the Nash equilibrium. Our theoretical analysis establishes that Nash-MP exhibits last-iterate linear convergence towards the $\beta$-regularized Nash equilibrium. Specifically, we prove that the KL-divergence to the optimal policy decreases at a rate of order $(1+2\beta)^{-N/2}$, where $N$ is a number of preference queries. We further demonstrate last-iterate linear convergence for the exploitability gap and uniformly for the span semi-norm of log-probabilities, with all these rates being independent of the size of the action space. Furthermore, we propose and analyze an approximate version of Nash-MP where proximal steps are estimated using stochastic policy gradients, making the algorithm closer to applications. Finally, we detail a practical implementation strategy for fine-tuning large language models and present experiments that demonstrate its competitive performance and compatibility with existing methods.

Weighted mesh algorithms for general Markov decision processes: Convergence and tractability

We introduce a mesh-type approach for tackling discrete-time, finite-horizon Markov Decision Processes (MDPs) characterized by state and action spaces that are general, encompassing both finite and infinite (yet suitably regular) subsets of Euclidean space. In particular, for bounded state and action spaces, our algorithm achieves a computational complexity that is tractable in the sense of Novak and Wozniakowski, and is polynomial in the time horizon. For unbounded state space the algorithm is "semi-tractable" in the sense that the complexity is proportional to $\epsilon^{-c}$ with some dimension independent $c\geq2$, for achieving an accuracy $\epsilon$, and polynomial in the time horizon with degree linear in the underlying dimension. As such the proposed approach has some flavor of the randomization method by Rust which deals with infinite horizon MDPs and uniform sampling in compact state space. However, the present approach is essentially different due to the finite horizon and a simulation procedure due to general transition distributions, and more general in the sense that it encompasses unbounded state space. To demonstrate the effectiveness of our algorithm, we provide illustrations based on Linear-Quadratic Gaussian (LQG) control problems.

Model-free Posterior Sampling via Learning Rate Randomization

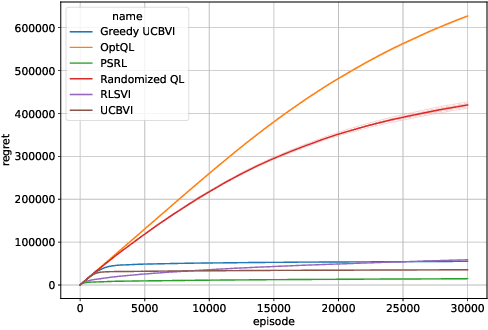
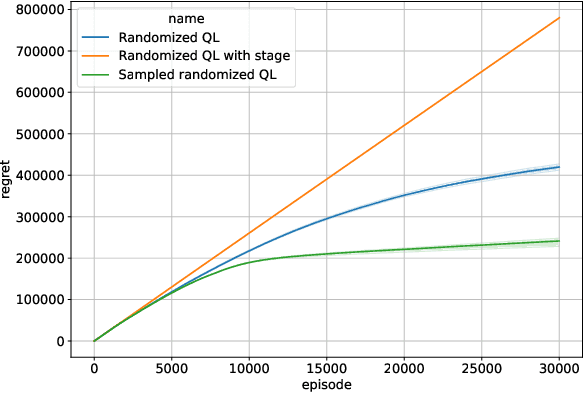
In this paper, we introduce Randomized Q-learning (RandQL), a novel randomized model-free algorithm for regret minimization in episodic Markov Decision Processes (MDPs). To the best of our knowledge, RandQL is the first tractable model-free posterior sampling-based algorithm. We analyze the performance of RandQL in both tabular and non-tabular metric space settings. In tabular MDPs, RandQL achieves a regret bound of order $\widetilde{\mathcal{O}}(\sqrt{H^{5}SAT})$, where $H$ is the planning horizon, $S$ is the number of states, $A$ is the number of actions, and $T$ is the number of episodes. For a metric state-action space, RandQL enjoys a regret bound of order $\widetilde{\mathcal{O}}(H^{5/2} T^{(d_z+1)/(d_z+2)})$, where $d_z$ denotes the zooming dimension. Notably, RandQL achieves optimistic exploration without using bonuses, relying instead on a novel idea of learning rate randomization. Our empirical study shows that RandQL outperforms existing approaches on baseline exploration environments.

Demonstration-Regularized RL

Incorporating expert demonstrations has empirically helped to improve the sample efficiency of reinforcement learning (RL). This paper quantifies theoretically to what extent this extra information reduces RL's sample complexity. In particular, we study the demonstration-regularized reinforcement learning that leverages the expert demonstrations by KL-regularization for a policy learned by behavior cloning. Our findings reveal that using $N^{\mathrm{E}}$ expert demonstrations enables the identification of an optimal policy at a sample complexity of order $\widetilde{\mathcal{O}}(\mathrm{Poly}(S,A,H)/(\varepsilon^2 N^{\mathrm{E}}))$ in finite and $\widetilde{\mathcal{O}}(\mathrm{Poly}(d,H)/(\varepsilon^2 N^{\mathrm{E}}))$ in linear Markov decision processes, where $\varepsilon$ is the target precision, $H$ the horizon, $A$ the number of action, $S$ the number of states in the finite case and $d$ the dimension of the feature space in the linear case. As a by-product, we provide tight convergence guarantees for the behaviour cloning procedure under general assumptions on the policy classes. Additionally, we establish that demonstration-regularized methods are provably efficient for reinforcement learning from human feedback (RLHF). In this respect, we provide theoretical evidence showing the benefits of KL-regularization for RLHF in tabular and linear MDPs. Interestingly, we avoid pessimism injection by employing computationally feasible regularization to handle reward estimation uncertainty, thus setting our approach apart from the prior works.

Sharp Deviations Bounds for Dirichlet Weighted Sums with Application to analysis of Bayesian algorithms

In this work, we derive sharp non-asymptotic deviation bounds for weighted sums of Dirichlet random variables. These bounds are based on a novel integral representation of the density of a weighted Dirichlet sum. This representation allows us to obtain a Gaussian-like approximation for the sum distribution using geometry and complex analysis methods. Our results generalize similar bounds for the Beta distribution obtained in the seminal paper Alfers and Dinges [1984]. Additionally, our results can be considered a sharp non-asymptotic version of the inverse of Sanov's theorem studied by Ganesh and O'Connell [1999] in the Bayesian setting. Based on these results, we derive new deviation bounds for the Dirichlet process posterior means with application to Bayesian bootstrap. Finally, we apply our estimates to the analysis of the Multinomial Thompson Sampling (TS) algorithm in multi-armed bandits and significantly sharpen the existing regret bounds by making them independent of the size of the arms distribution support.

Theoretical guarantees for neural control variates in MCMC

In this paper, we propose a variance reduction approach for Markov chains based on additive control variates and the minimization of an appropriate estimate for the asymptotic variance. We focus on the particular case when control variates are represented as deep neural networks. We derive the optimal convergence rate of the asymptotic variance under various ergodicity assumptions on the underlying Markov chain. The proposed approach relies upon recent results on the stochastic errors of variance reduction algorithms and function approximation theory.

Fast Rates for Maximum Entropy Exploration

We consider the reinforcement learning (RL) setting, in which the agent has to act in unknown environment driven by a Markov Decision Process (MDP) with sparse or even reward free signals. In this situation, exploration becomes the main challenge. In this work, we study the maximum entropy exploration problem of two different types. The first type is visitation entropy maximization that was previously considered by Hazan et al. (2019) in the discounted setting. For this type of exploration, we propose an algorithm based on a game theoretic representation that has $\widetilde{\mathcal{O}}(H^3 S^2 A / \varepsilon^2)$ sample complexity thus improving the $\varepsilon$-dependence of Hazan et al. (2019), where $S$ is a number of states, $A$ is a number of actions, $H$ is an episode length, and $\varepsilon$ is a desired accuracy. The second type of entropy we study is the trajectory entropy. This objective function is closely related to the entropy-regularized MDPs, and we propose a simple modification of the UCBVI algorithm that has a sample complexity of order $\widetilde{\mathcal{O}}(1/\varepsilon)$ ignoring dependence in $S, A, H$. Interestingly enough, it is the first theoretical result in RL literature establishing that the exploration problem for the regularized MDPs can be statistically strictly easier (in terms of sample complexity) than for the ordinary MDPs.

Primal-dual regression approach for Markov decision processes with general state and action space

We develop a regression based primal-dual martingale approach for solving finite time horizon MDPs with general state and action space. As a result, our method allows for the construction of tight upper and lower biased approximations of the value functions, and, provides tight approximations to the optimal policy. In particular, we prove tight error bounds for the estimated duality gap featuring polynomial dependence on the time horizon, and sublinear dependence on the cardinality/dimension of the possibly infinite state and action space.From a computational point of view the proposed method is efficient since, in contrast to usual duality-based methods for optimal control problems in the literature, the Monte Carlo procedures here involved do not require nested simulations.

Optimistic Posterior Sampling for Reinforcement Learning with Few Samples and Tight Guarantees

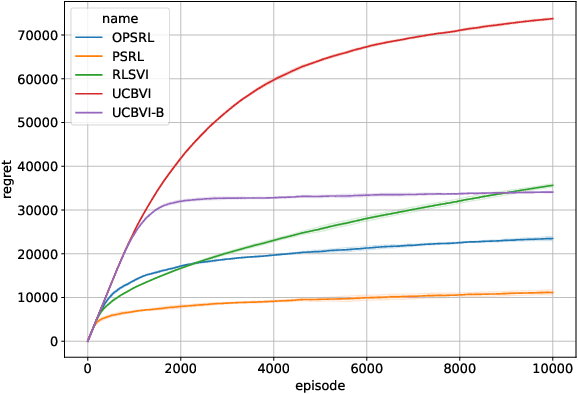
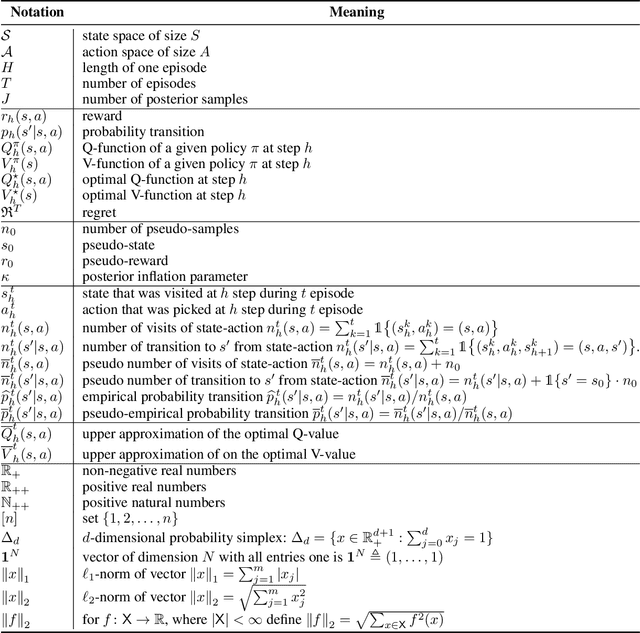
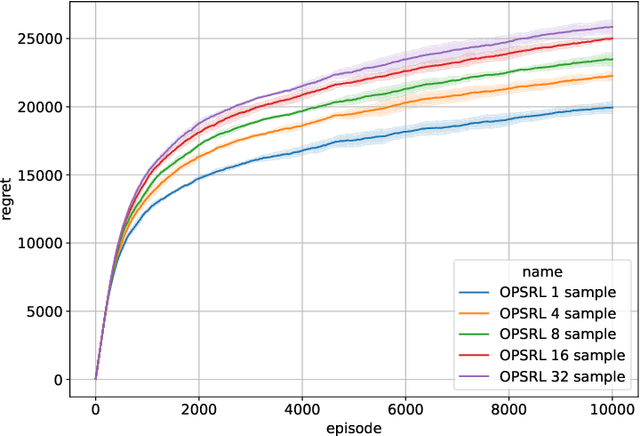
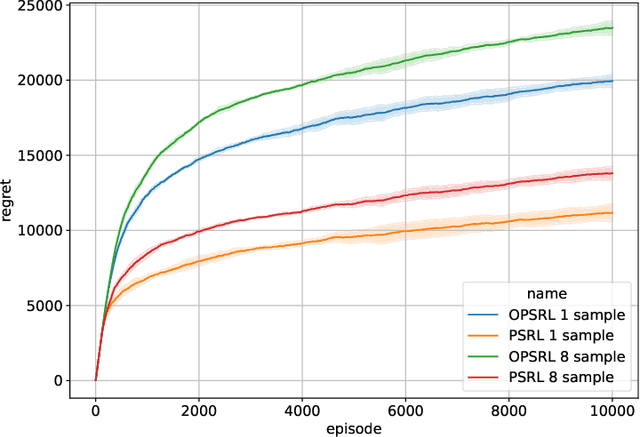
We consider reinforcement learning in an environment modeled by an episodic, finite, stage-dependent Markov decision process of horizon $H$ with $S$ states, and $A$ actions. The performance of an agent is measured by the regret after interacting with the environment for $T$ episodes. We propose an optimistic posterior sampling algorithm for reinforcement learning (OPSRL), a simple variant of posterior sampling that only needs a number of posterior samples logarithmic in $H$, $S$, $A$, and $T$ per state-action pair. For OPSRL we guarantee a high-probability regret bound of order at most $\widetilde{\mathcal{O}}(\sqrt{H^3SAT})$ ignoring $\text{poly}\log(HSAT)$ terms. The key novel technical ingredient is a new sharp anti-concentration inequality for linear forms which may be of independent interest. Specifically, we extend the normal approximation-based lower bound for Beta distributions by Alfers and Dinges [1984] to Dirichlet distributions. Our bound matches the lower bound of order $\Omega(\sqrt{H^3SAT})$, thereby answering the open problems raised by Agrawal and Jia [2017b] for the episodic setting.