Weighted mesh algorithms for general Markov decision processes: Convergence and tractability

We introduce a mesh-type approach for tackling discrete-time, finite-horizon Markov Decision Processes (MDPs) characterized by state and action spaces that are general, encompassing both finite and infinite (yet suitably regular) subsets of Euclidean space. In particular, for bounded state and action spaces, our algorithm achieves a computational complexity that is tractable in the sense of Novak and Wozniakowski, and is polynomial in the time horizon. For unbounded state space the algorithm is "semi-tractable" in the sense that the complexity is proportional to $\epsilon^{-c}$ with some dimension independent $c\geq2$, for achieving an accuracy $\epsilon$, and polynomial in the time horizon with degree linear in the underlying dimension. As such the proposed approach has some flavor of the randomization method by Rust which deals with infinite horizon MDPs and uniform sampling in compact state space. However, the present approach is essentially different due to the finite horizon and a simulation procedure due to general transition distributions, and more general in the sense that it encompasses unbounded state space. To demonstrate the effectiveness of our algorithm, we provide illustrations based on Linear-Quadratic Gaussian (LQG) control problems.

Primal-dual regression approach for Markov decision processes with general state and action space

We develop a regression based primal-dual martingale approach for solving finite time horizon MDPs with general state and action space. As a result, our method allows for the construction of tight upper and lower biased approximations of the value functions, and, provides tight approximations to the optimal policy. In particular, we prove tight error bounds for the estimated duality gap featuring polynomial dependence on the time horizon, and sublinear dependence on the cardinality/dimension of the possibly infinite state and action space.From a computational point of view the proposed method is efficient since, in contrast to usual duality-based methods for optimal control problems in the literature, the Monte Carlo procedures here involved do not require nested simulations.

Reinforced optimal control

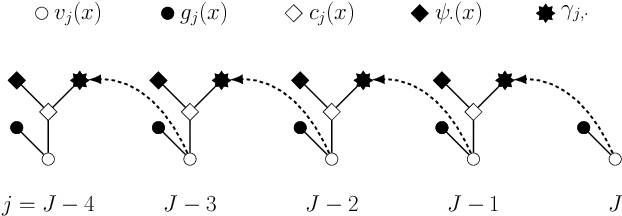
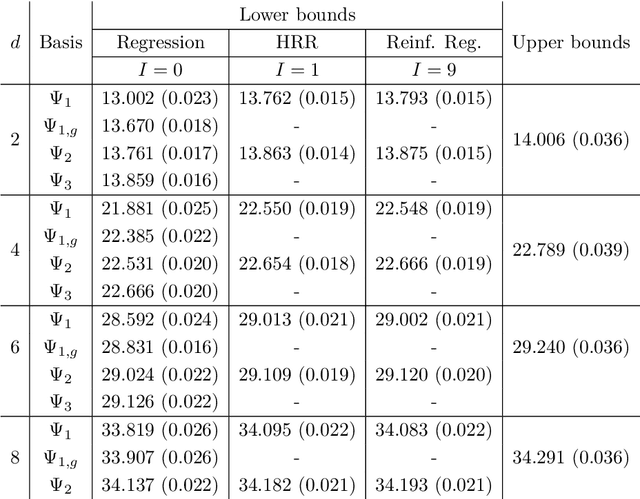
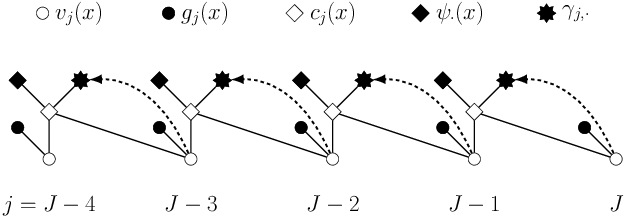
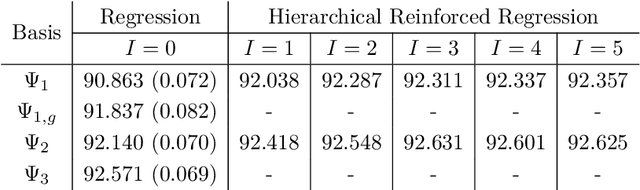
Least squares Monte Carlo methods are a popular numerical approximation method for solving stochastic control problems. Based on dynamic programming, their key feature is the approximation of the conditional expectation of future rewards by linear least squares regression. Hence, the choice of basis functions is crucial for the accuracy of the method. Earlier work by some of us [Belomestny, Schoenmakers, Spokoiny, Zharkynbay. Commun.~Math.~Sci., 18(1):109-121, 2020] proposes to \emph{reinforce} the basis functions in the case of optimal stopping problems by already computed value functions for later times, thereby considerably improving the accuracy with limited additional computational cost. We extend the reinforced regression method to a general class of stochastic control problems, while considerably improving the method's efficiency, as demonstrated by substantial numerical examples as well as theoretical analysis.

Optimal stopping via reinforced regression

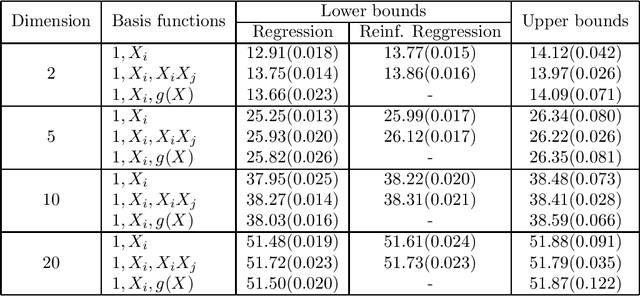
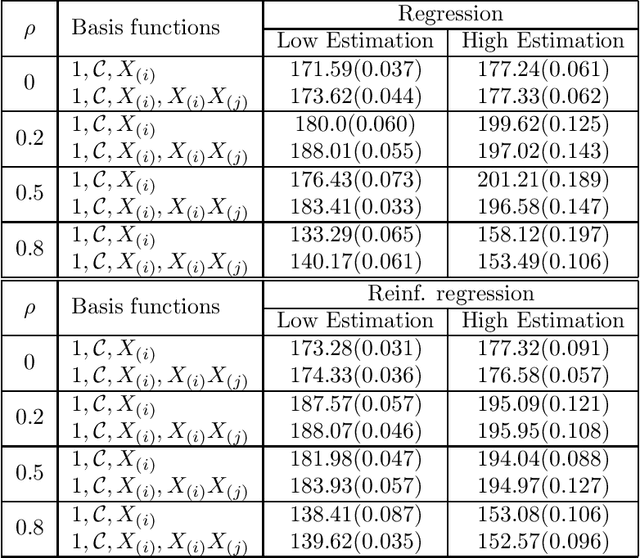
In this note we propose a new approach towards solving numerically optimal stopping problems via reinforced regression based Monte Carlo algorithms. The main idea of the method is to reinforce standard linear regression algorithms in each backward induction step by adding new basis functions based on previously estimated continuation values. The proposed methodology is illustrated by a numerical example from mathematical finance.