High dimensional change-point detection: a complete graph approach

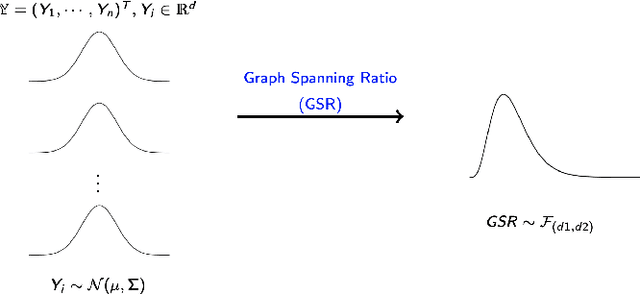
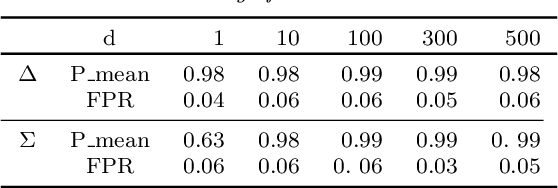
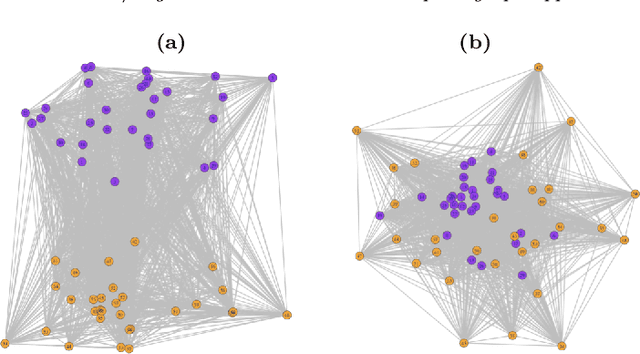
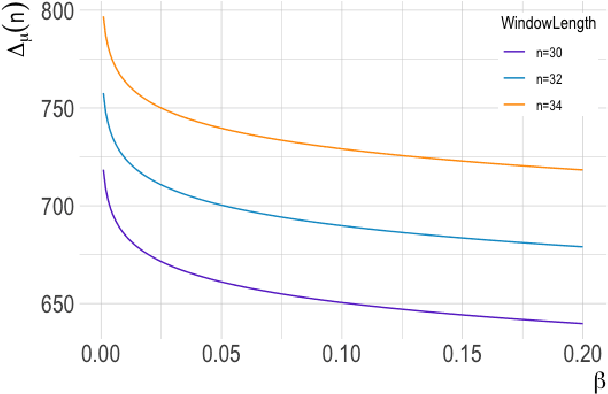
The aim of online change-point detection is for a accurate, timely discovery of structural breaks. As data dimension outgrows the number of data in observation, online detection becomes challenging. Existing methods typically test only the change of mean, which omit the practical aspect of change of variance. We propose a complete graph-based, change-point detection algorithm to detect change of mean and variance from low to high-dimensional online data with a variable scanning window. Inspired by complete graph structure, we introduce graph-spanning ratios to map high-dimensional data into metrics, and then test statistically if a change of mean or change of variance occurs. Theoretical study shows that our approach has the desirable pivotal property and is powerful with prescribed error probabilities. We demonstrate that this framework outperforms other methods in terms of detection power. Our approach has high detection power with small and multiple scanning window, which allows timely detection of change-point in the online setting. Finally, we applied the method to financial data to detect change-points in S&P 500 stocks.

Reinforced optimal control

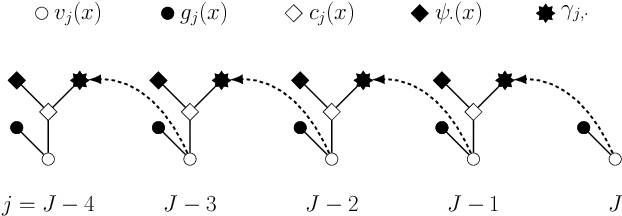
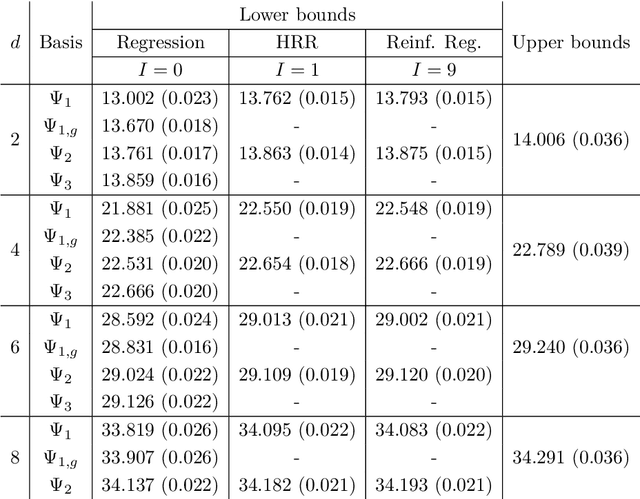
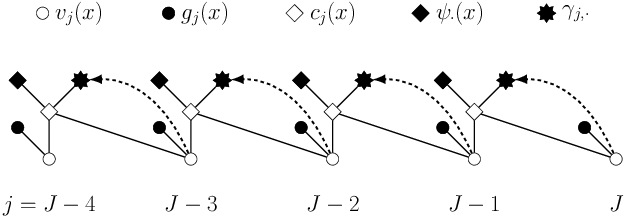
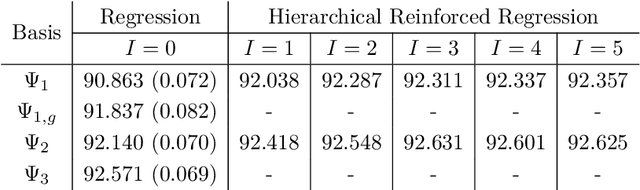
Least squares Monte Carlo methods are a popular numerical approximation method for solving stochastic control problems. Based on dynamic programming, their key feature is the approximation of the conditional expectation of future rewards by linear least squares regression. Hence, the choice of basis functions is crucial for the accuracy of the method. Earlier work by some of us [Belomestny, Schoenmakers, Spokoiny, Zharkynbay. Commun.~Math.~Sci., 18(1):109-121, 2020] proposes to \emph{reinforce} the basis functions in the case of optimal stopping problems by already computed value functions for later times, thereby considerably improving the accuracy with limited additional computational cost. We extend the reinforced regression method to a general class of stochastic control problems, while considerably improving the method's efficiency, as demonstrated by substantial numerical examples as well as theoretical analysis.

Structure-adaptive manifold estimation

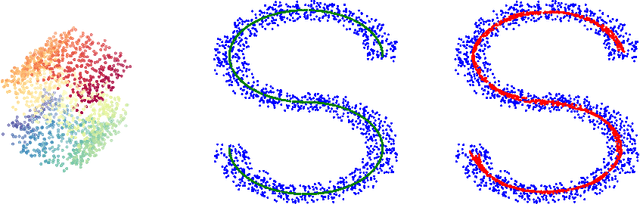
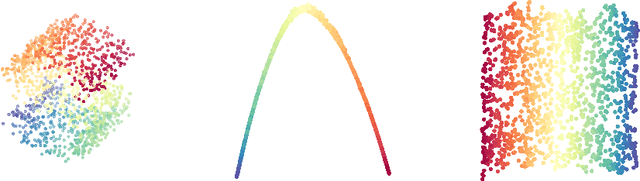
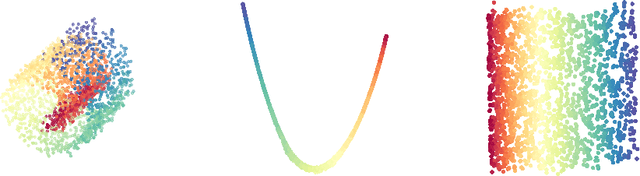
We consider a problem of manifold estimation from noisy observations. We suggest a novel adaptive procedure, which simultaneously reconstructs a smooth manifold from the observations and estimates projectors onto the tangent spaces. Many manifold learning procedures locally approximate a manifold by a weighted average over a small neighborhood. However, in the presence of large noise, the assigned weights become so corrupted that the averaged estimate shows very poor performance. We adjust the weights so they capture the manifold structure better. We propose a computationally efficient procedure, which iteratively refines the weights on each step, such that, after several iterations, we obtain the "oracle" weights, so the quality of the final estimates does not suffer even in the presence of relatively large noise. We also provide a theoretical study of the procedure and prove its optimality deriving both new upper and lower bounds for manifold estimation under the Hausdorff loss.

Optimal stopping via reinforced regression

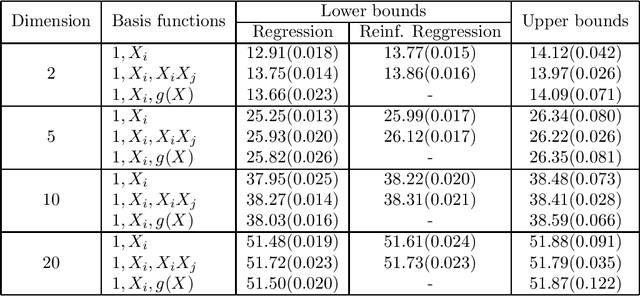
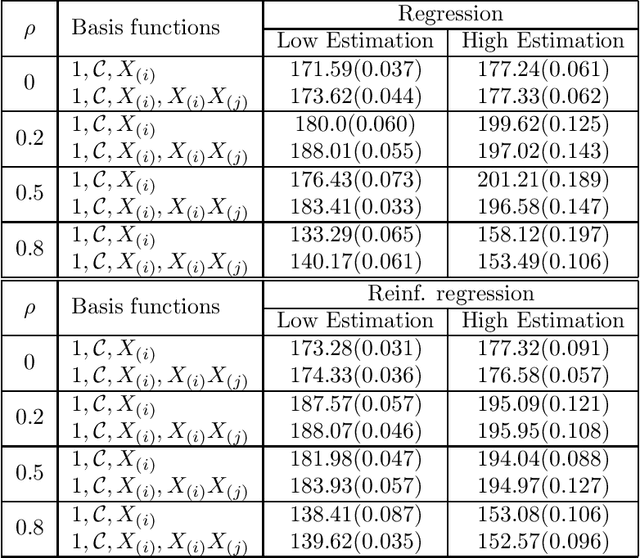
In this note we propose a new approach towards solving numerically optimal stopping problems via reinforced regression based Monte Carlo algorithms. The main idea of the method is to reinforce standard linear regression algorithms in each backward induction step by adding new basis functions based on previously estimated continuation values. The proposed methodology is illustrated by a numerical example from mathematical finance.

Pointwise adaptation via stagewise aggregation of local estimates for multiclass classification

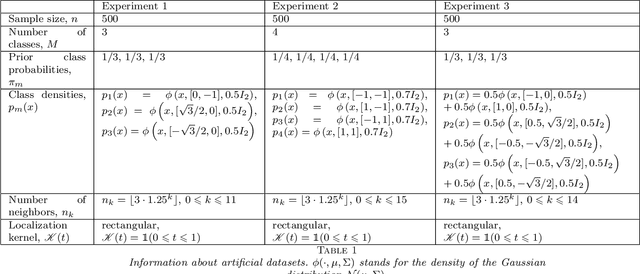
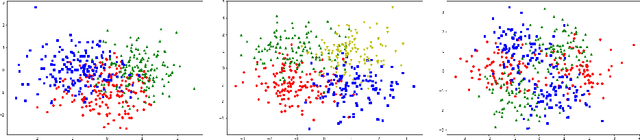
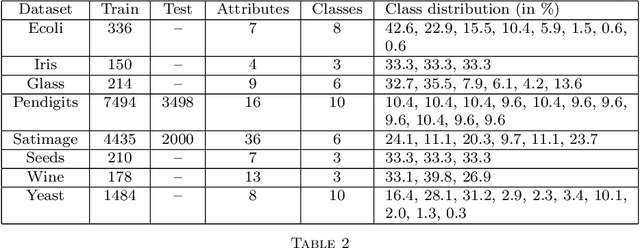
We consider a problem of multiclass classification, where the training sample $S_n = \{(X_i, Y_i)\}_{i=1}^n$ is generated from the model $\mathbb p(Y = m | X = x) = \theta_m(x)$, $1 \leq m \leq M$, and $\theta_1(x), \dots, \theta_M(x)$ are unknown Lipschitz functions. Given a test point $X$, our goal is to estimate $\theta_1(X), \dots, \theta_M(X)$. An approach based on nonparametric smoothing uses a localization technique, i.e. the weight of observation $(X_i, Y_i)$ depends on the distance between $X_i$ and $X$. However, local estimates strongly depend on localizing scheme. In our solution we fix several schemes $W_1, \dots, W_K$, compute corresponding local estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ for each of them and apply an aggregation procedure. We propose an algorithm, which constructs a convex combination of the estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ such that the aggregated estimate behaves approximately as well as the best one from the collection $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$. We also study theoretical properties of the procedure, prove oracle results and establish rates of convergence under mild assumptions.

Adaptive Nonparametric Clustering

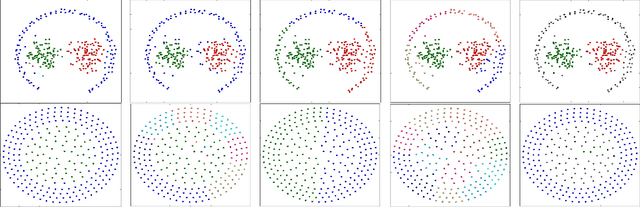
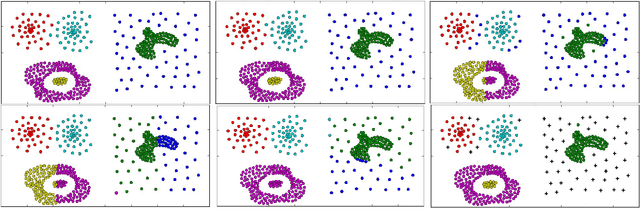
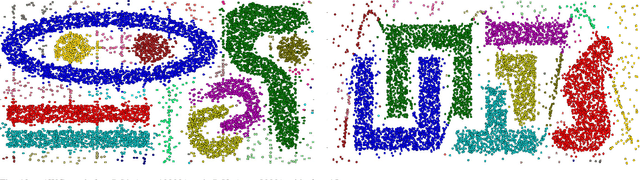
This paper presents a new approach to non-parametric cluster analysis called Adaptive Weights Clustering (AWC). The idea is to identify the clustering structure by checking at different points and for different scales on departure from local homogeneity. The proposed procedure describes the clustering structure in terms of weights \( w_{ij} \) each of them measures the degree of local inhomogeneity for two neighbor local clusters using statistical tests of "no gap" between them. % The procedure starts from very local scale, then the parameter of locality grows by some factor at each step. The method is fully adaptive and does not require to specify the number of clusters or their structure. The clustering results are not sensitive to noise and outliers, the procedure is able to recover different clusters with sharp edges or manifold structure. The method is scalable and computationally feasible. An intensive numerical study shows a state-of-the-art performance of the method in various artificial examples and applications to text data. Our theoretical study states optimal sensitivity of AWC to local inhomogeneity.

Sparse Non Gaussian Component Analysis by Semidefinite Programming

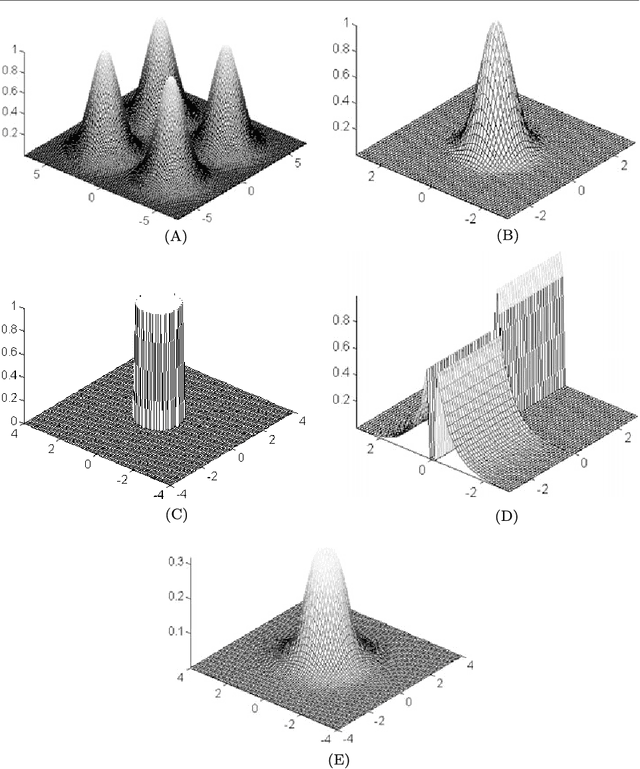
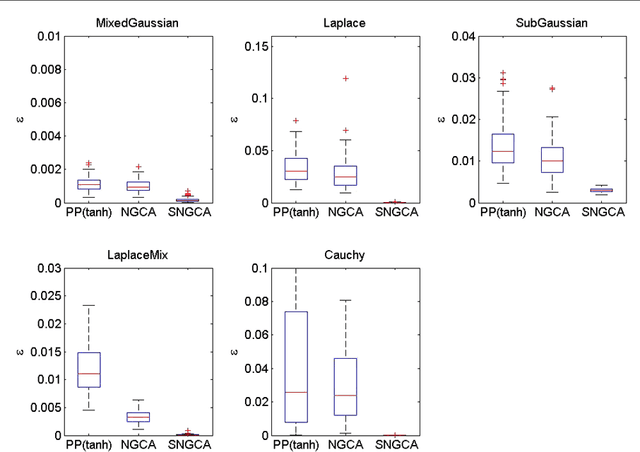
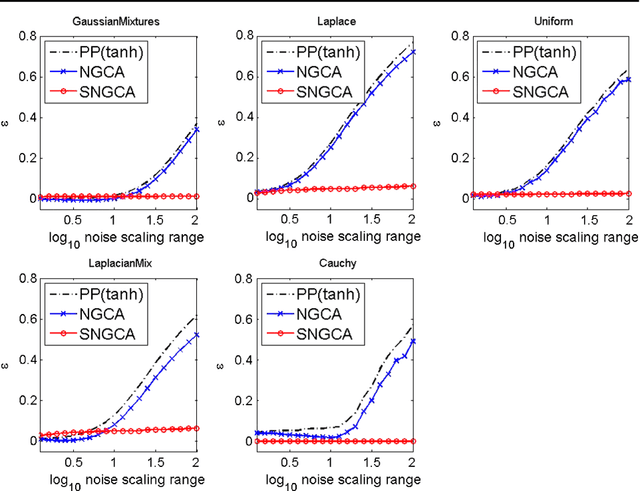
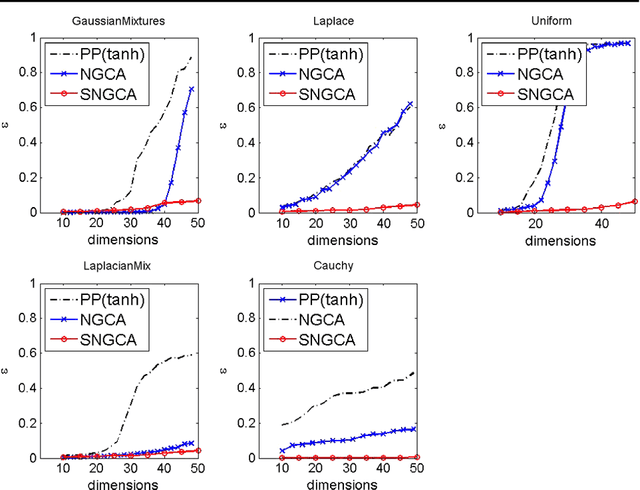
Sparse non-Gaussian component analysis (SNGCA) is an unsupervised method of extracting a linear structure from a high dimensional data based on estimating a low-dimensional non-Gaussian data component. In this paper we discuss a new approach to direct estimation of the projector on the target space based on semidefinite programming which improves the method sensitivity to a broad variety of deviations from normality. We also discuss the procedures which allows to recover the structure when its effective dimension is unknown.