Score-based change point detection via tracking the best of infinitely many experts

We suggest a novel algorithm for online change point detection based on sequential score function estimation and tracking the best expert approach. The core of the procedure is a version of the fixed share forecaster for the case of infinite number of experts and quadratic loss functions. The algorithm shows a promising performance in numerical experiments on artificial and real-world data sets. We also derive new upper bounds on the dynamic regret of the fixed share forecaster with varying parameter, which are of independent interest.

Dimension-free Structured Covariance Estimation

Given a sample of i.i.d. high-dimensional centered random vectors, we consider a problem of estimation of their covariance matrix $\Sigma$ with an additional assumption that $\Sigma$ can be represented as a sum of a few Kronecker products of smaller matrices. Under mild conditions, we derive the first non-asymptotic dimension-free high-probability bound on the Frobenius distance between $\Sigma$ and a widely used penalized permuted least squares estimate. Because of the hidden structure, the established rate of convergence is faster than in the standard covariance estimation problem.

Breaking the Heavy-Tailed Noise Barrier in Stochastic Optimization Problems

We consider stochastic optimization problems with heavy-tailed noise with structured density. For such problems, we show that it is possible to get faster rates of convergence than $\mathcal{O}(K^{-2(\alpha - 1)/\alpha})$, when the stochastic gradients have finite moments of order $\alpha \in (1, 2]$. In particular, our analysis allows the noise norm to have an unbounded expectation. To achieve these results, we stabilize stochastic gradients, using smoothed medians of means. We prove that the resulting estimates have negligible bias and controllable variance. This allows us to carefully incorporate them into clipped-SGD and clipped-SSTM and derive new high-probability complexity bounds in the considered setup.

Exploring Local Norms in Exp-concave Statistical Learning

We consider the problem of stochastic convex optimization with exp-concave losses using Empirical Risk Minimization in a convex class. Answering a question raised in several prior works, we provide a $O( d / n + \log( 1 / \delta) / n )$ excess risk bound valid for a wide class of bounded exp-concave losses, where $d$ is the dimension of the convex reference set, $n$ is the sample size, and $\delta$ is the confidence level. Our result is based on a unified geometric assumption on the gradient of losses and the notion of local norms.

A Contrastive Approach to Online Change Point Detection

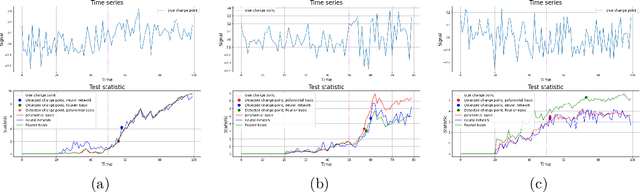
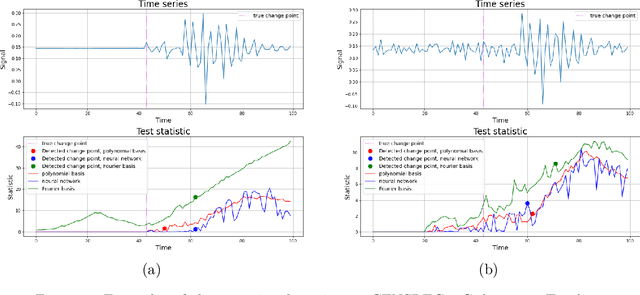
We suggest a novel procedure for online change point detection. Our approach expands an idea of maximizing a discrepancy measure between points from pre-change and post-change distributions. This leads to a flexible procedure suitable for both parametric and nonparametric scenarios. We prove non-asymptotic bounds on the average running length of the procedure and its expected detection delay. The efficiency of the algorithm is illustrated with numerical experiments on synthetic and real-world data sets.

Exponential Savings in Agnostic Active Learning through Abstention

We show that in pool-based active classification without assumptions on the underlying distribution, if the learner is given the power to abstain from some predictions by paying the price marginally smaller than the average loss $1/2$ of a random guess, exponential savings in the number of label requests are possible whenever they are possible in the corresponding realizable problem. We extend this result to provide a necessary and sufficient condition for exponential savings in pool-based active classification under the model misspecification.

Rates of convergence for density estimation with GANs

We undertake a precise study of the non-asymptotic properties of vanilla generative adversarial networks (GANs) and derive theoretical guarantees in the problem of estimating an unknown $d$-dimensional density $p^*$ under a proper choice of the class of generators and discriminators. We prove that the resulting density estimate converges to $p^*$ in terms of Jensen-Shannon (JS) divergence at the rate $(\log n/n)^{2\beta/(2\beta+d)}$ where $n$ is the sample size and $\beta$ determines the smoothness of $p^*.$ This is the first result in the literature on density estimation using vanilla GANs with JS rates faster than $n^{-1/2}$ in the regime $\beta>d/2.$

Structure-adaptive manifold estimation

We consider a problem of manifold estimation from noisy observations. We suggest a novel adaptive procedure, which simultaneously reconstructs a smooth manifold from the observations and estimates projectors onto the tangent spaces. Many manifold learning procedures locally approximate a manifold by a weighted average over a small neighborhood. However, in the presence of large noise, the assigned weights become so corrupted that the averaged estimate shows very poor performance. We adjust the weights so they capture the manifold structure better. We propose a computationally efficient procedure, which iteratively refines the weights on each step, such that, after several iterations, we obtain the "oracle" weights, so the quality of the final estimates does not suffer even in the presence of relatively large noise. We also provide a theoretical study of the procedure and prove its optimality deriving both new upper and lower bounds for manifold estimation under the Hausdorff loss.

Pointwise adaptation via stagewise aggregation of local estimates for multiclass classification

We consider a problem of multiclass classification, where the training sample $S_n = \{(X_i, Y_i)\}_{i=1}^n$ is generated from the model $\mathbb p(Y = m | X = x) = \theta_m(x)$, $1 \leq m \leq M$, and $\theta_1(x), \dots, \theta_M(x)$ are unknown Lipschitz functions. Given a test point $X$, our goal is to estimate $\theta_1(X), \dots, \theta_M(X)$. An approach based on nonparametric smoothing uses a localization technique, i.e. the weight of observation $(X_i, Y_i)$ depends on the distance between $X_i$ and $X$. However, local estimates strongly depend on localizing scheme. In our solution we fix several schemes $W_1, \dots, W_K$, compute corresponding local estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ for each of them and apply an aggregation procedure. We propose an algorithm, which constructs a convex combination of the estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ such that the aggregated estimate behaves approximately as well as the best one from the collection $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$. We also study theoretical properties of the procedure, prove oracle results and establish rates of convergence under mild assumptions.