Structure-adaptive manifold estimation
Paper and Code
Jun 19, 2019
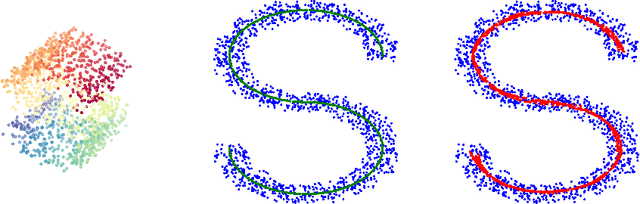
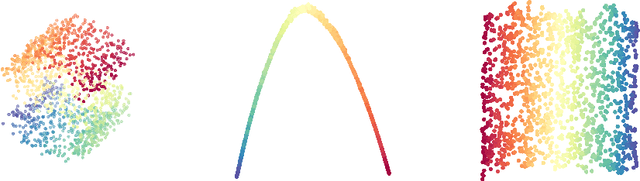
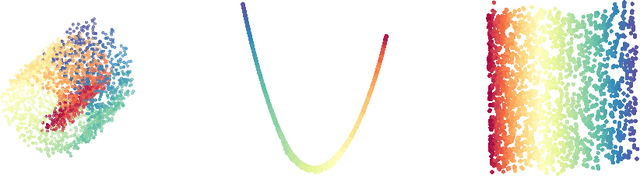
We consider a problem of manifold estimation from noisy observations. We suggest a novel adaptive procedure, which simultaneously reconstructs a smooth manifold from the observations and estimates projectors onto the tangent spaces. Many manifold learning procedures locally approximate a manifold by a weighted average over a small neighborhood. However, in the presence of large noise, the assigned weights become so corrupted that the averaged estimate shows very poor performance. We adjust the weights so they capture the manifold structure better. We propose a computationally efficient procedure, which iteratively refines the weights on each step, such that, after several iterations, we obtain the "oracle" weights, so the quality of the final estimates does not suffer even in the presence of relatively large noise. We also provide a theoretical study of the procedure and prove its optimality deriving both new upper and lower bounds for manifold estimation under the Hausdorff loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge