Pointwise adaptation via stagewise aggregation of local estimates for multiclass classification
Paper and Code
Apr 08, 2018

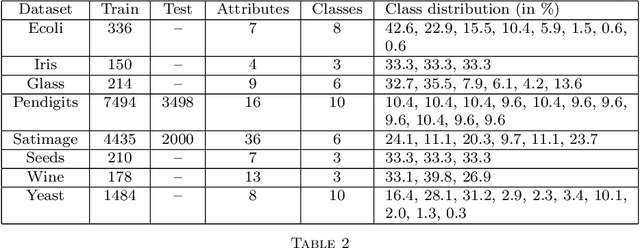
We consider a problem of multiclass classification, where the training sample $S_n = \{(X_i, Y_i)\}_{i=1}^n$ is generated from the model $\mathbb p(Y = m | X = x) = \theta_m(x)$, $1 \leq m \leq M$, and $\theta_1(x), \dots, \theta_M(x)$ are unknown Lipschitz functions. Given a test point $X$, our goal is to estimate $\theta_1(X), \dots, \theta_M(X)$. An approach based on nonparametric smoothing uses a localization technique, i.e. the weight of observation $(X_i, Y_i)$ depends on the distance between $X_i$ and $X$. However, local estimates strongly depend on localizing scheme. In our solution we fix several schemes $W_1, \dots, W_K$, compute corresponding local estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ for each of them and apply an aggregation procedure. We propose an algorithm, which constructs a convex combination of the estimates $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$ such that the aggregated estimate behaves approximately as well as the best one from the collection $\widetilde\theta^{(1)}, \dots, \widetilde\theta^{(K)}$. We also study theoretical properties of the procedure, prove oracle results and establish rates of convergence under mild assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge