Generalized generalized linear models: Convex estimation and online bounds

We introduce a new computational framework for estimating parameters in generalized generalized linear models (GGLM), a class of models that extends the popular generalized linear models (GLM) to account for dependencies among observations in spatio-temporal data. The proposed approach uses a monotone operator-based variational inequality method to overcome non-convexity in parameter estimation and provide guarantees for parameter recovery. The results can be applied to GLM and GGLM, focusing on spatio-temporal models. We also present online instance-based bounds using martingale concentrations inequalities. Finally, we demonstrate the performance of the algorithm using numerical simulations and a real data example for wildfire incidents.

Convex Recovery of Marked Spatio-Temporal Point Processes

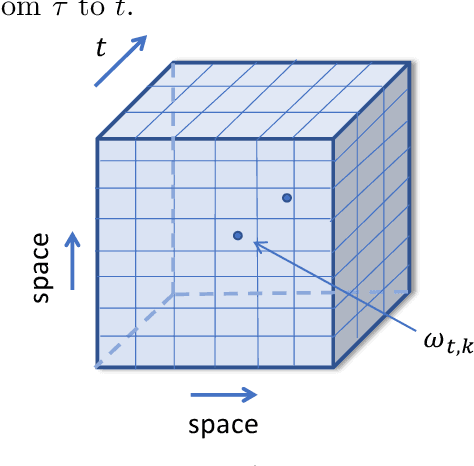
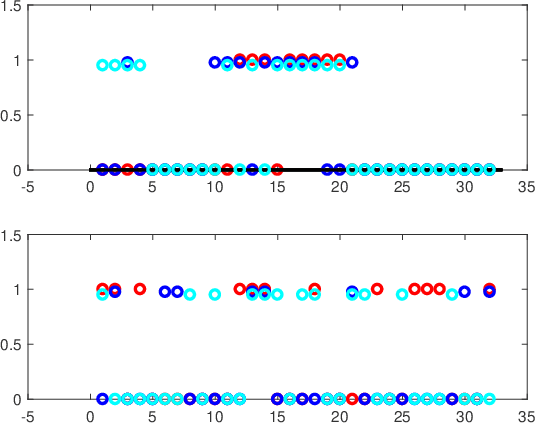
We present a multi-dimensional Bernoulli process model for spatial-temporal discrete event data with categorical marks, where the probability of an event of a specific category in a location may be influenced by past events at this and other locations. The focus is to introduce general forms of influence function which can capture an arbitrary shape of influence from historical events, between locations, and between different categories of events. The general form of influence function differs from the commonly adapted exponential delaying function over time, and more importantly, in our model, we can learn the delayed influence of prior events, which is an aspect seemingly largely ignored in prior literature. Prior knowledge or assumptions on the influence function are incorporated into our framework by allowing general convex constraints on the parameters specifying the influence function. We develop two approaches for recovering these parameters, using the constrained least-square (LS) and maximum likelihood (ML) estimations. We demonstrate the performance of our approach on synthetic examples and illustrate its promise using real data (crime data and novel coronavirus data), in extracting knowledge about the general influences and making predictions.

Adaptive Denoising of Signals with Shift-Invariant Structure

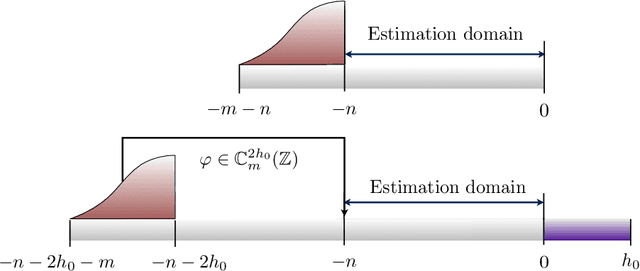
We study the problem of discrete-time signal denoising, following the line of research initiated by [Nem91] and further developed in [JN09, JN10, HJNO15, OHJN16]. Previous papers considered the following setup: the signal is assumed to admit a convolution-type linear oracle -- an unknown linear estimator in the form of the convolution of the observations with an unknown time-invariant filter with small $\ell_2$-norm. It was shown that such an oracle can be "mimicked" by an efficiently computable non-linear convolution-type estimator, in which the filter minimizes the Fourier-domain $\ell_\infty$-norm of the residual, regularized by the Fourier-domain $\ell_1$-norm of the filter. Following [OHJN16], here we study an alternative family of estimators, replacing the $\ell_\infty$-norm of the residual with the $\ell_2$-norm. Such estimators are found to have better statistical properties, in particular, we prove sharp oracle inequalities for their $\ell_2$-loss. Our guarantees require an extra assumption of approximate shift-invariance: the signal must be $\varkappa$-close, in $\ell_2$-metric, to some shift-invariant linear subspace with bounded dimension $s$. However, this subspace can be completely unknown, and the remainder terms in the oracle inequalities scale at most polynomially with $s$ and $\varkappa$. In conclusion, we show that the new assumption implies the previously considered one, providing explicit constructions of the convolution-type linear oracles with $\ell_2$-norm bounded in terms of parameters $s$ and $\varkappa$.

Conditional Gradient Algorithms for Norm-Regularized Smooth Convex Optimization

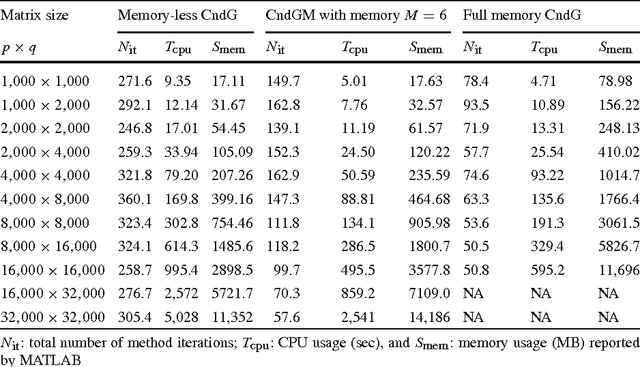
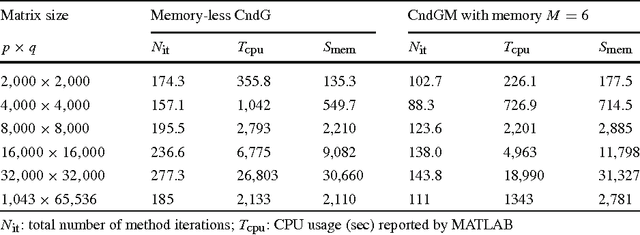
Motivated by some applications in signal processing and machine learning, we consider two convex optimization problems where, given a cone $K$, a norm $\|\cdot\|$ and a smooth convex function $f$, we want either 1) to minimize the norm over the intersection of the cone and a level set of $f$, or 2) to minimize over the cone the sum of $f$ and a multiple of the norm. We focus on the case where (a) the dimension of the problem is too large to allow for interior point algorithms, (b) $\|\cdot\|$ is "too complicated" to allow for computationally cheap Bregman projections required in the first-order proximal gradient algorithms. On the other hand, we assume that {it is relatively easy to minimize linear forms over the intersection of $K$ and the unit $\|\cdot\|$-ball}. Motivating examples are given by the nuclear norm with $K$ being the entire space of matrices, or the positive semidefinite cone in the space of symmetric matrices, and the Total Variation norm on the space of 2D images. We discuss versions of the Conditional Gradient algorithm capable to handle our problems of interest, provide the related theoretical efficiency estimates and outline some applications.

Accuracy guaranties for $\ell_1$ recovery of block-sparse signals

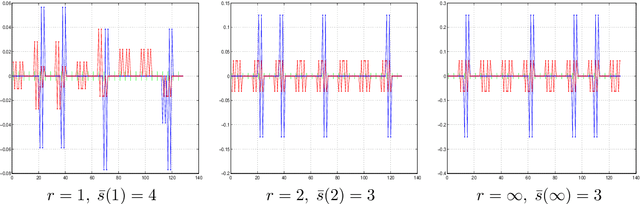
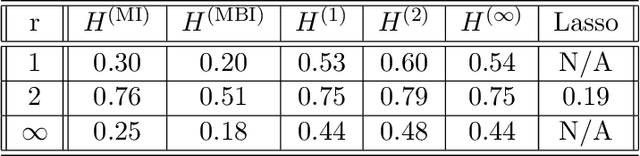
We introduce a general framework to handle structured models (sparse and block-sparse with possibly overlapping blocks). We discuss new methods for their recovery from incomplete observation, corrupted with deterministic and stochastic noise, using block-$\ell_1$ regularization. While the current theory provides promising bounds for the recovery errors under a number of different, yet mostly hard to verify conditions, our emphasis is on verifiable conditions on the problem parameters (sensing matrix and the block structure) which guarantee accurate recovery. Verifiability of our conditions not only leads to efficiently computable bounds for the recovery error but also allows us to optimize these error bounds with respect to the method parameters, and therefore construct estimators with improved statistical properties. To justify our approach, we also provide an oracle inequality, which links the properties of the proposed recovery algorithms and the best estimation performance. Furthermore, utilizing these verifiable conditions, we develop a computationally cheap alternative to block-$\ell_1$ minimization, the non-Euclidean Block Matching Pursuit algorithm. We close by presenting a numerical study to investigate the effect of different block regularizations and demonstrate the performance of the proposed recoveries.

On unified view of nullspace-type conditions for recoveries associated with general sparsity structures

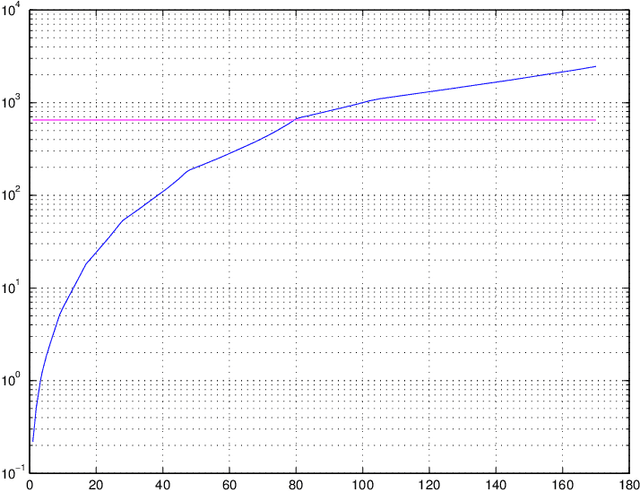
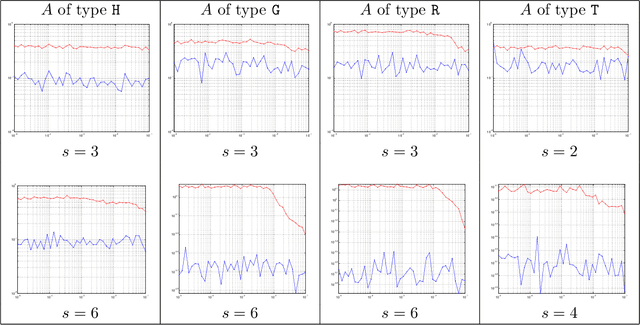
We discuss a general notion of "sparsity structure" and associated recoveries of a sparse signal from its linear image of reduced dimension possibly corrupted with noise. Our approach allows for unified treatment of (a) the "usual sparsity" and "usual $\ell_1$ recovery," (b) block-sparsity with possibly overlapping blocks and associated block-$\ell_1$ recovery, and (c) low-rank-oriented recovery by nuclear norm minimization. The proposed recovery routines are natural extensions of the usual $\ell_1$ minimization used in Compressed Sensing. Specifically we present nullspace-type sufficient conditions for the recovery to be precise on sparse signals in the noiseless case. Then we derive error bounds for imperfect (nearly sparse signal, presence of observation noise, etc.) recovery under these conditions. In all of these cases, we present efficiently verifiable sufficient conditions for the validity of the associated nullspace properties.

Sparse Non Gaussian Component Analysis by Semidefinite Programming

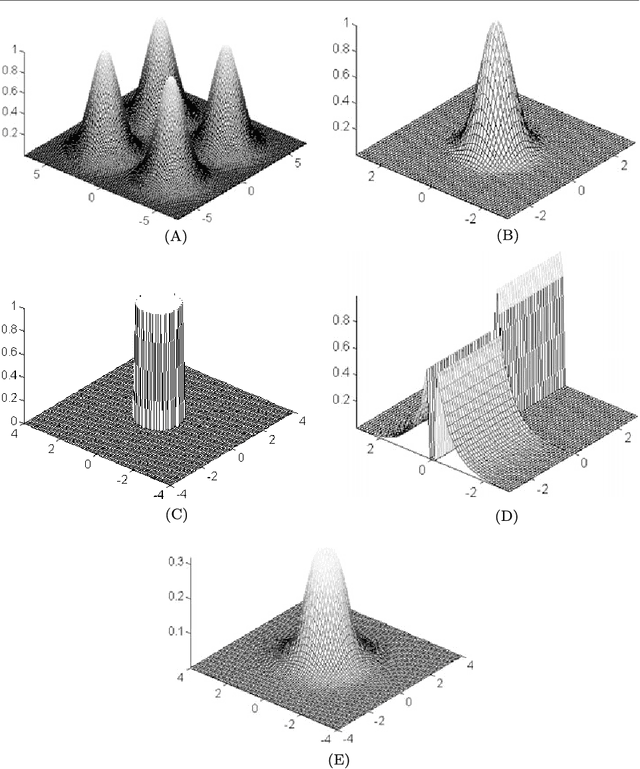
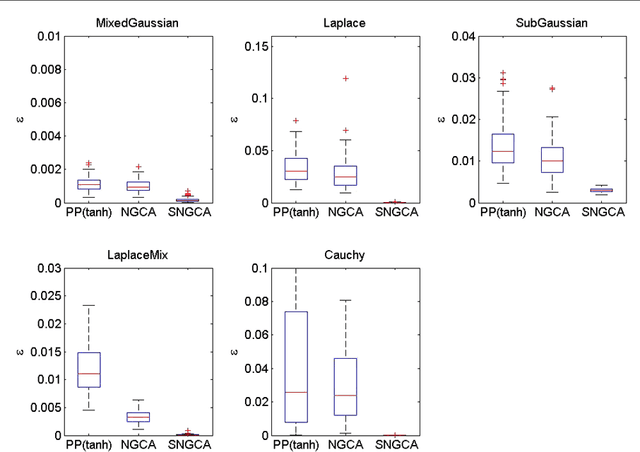
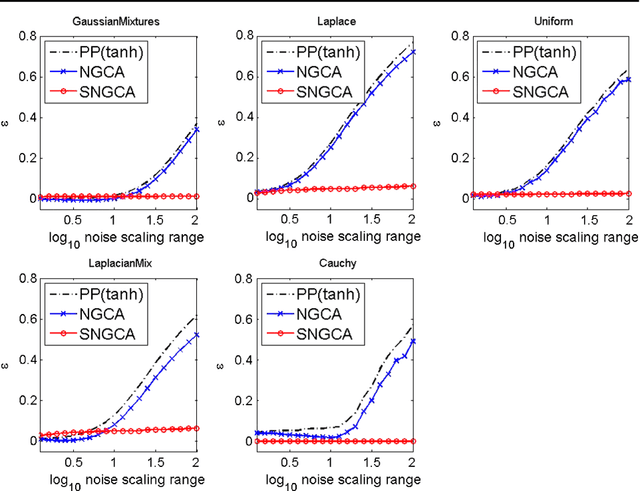
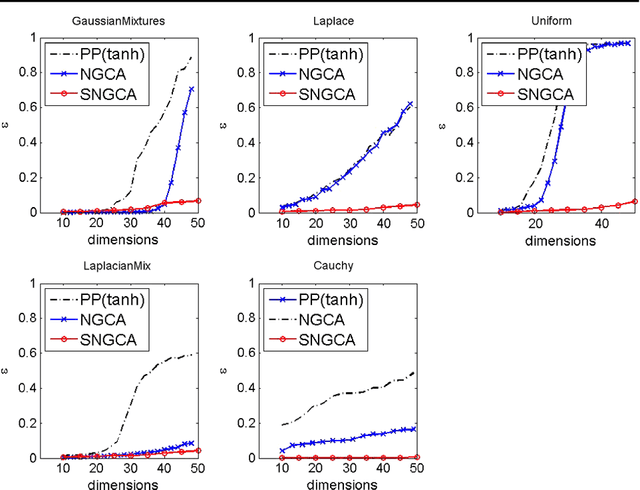
Sparse non-Gaussian component analysis (SNGCA) is an unsupervised method of extracting a linear structure from a high dimensional data based on estimating a low-dimensional non-Gaussian data component. In this paper we discuss a new approach to direct estimation of the projector on the target space based on semidefinite programming which improves the method sensitivity to a broad variety of deviations from normality. We also discuss the procedures which allows to recover the structure when its effective dimension is unknown.