Smooth Monotone Stochastic Variational Inequalities and Saddle Point Problems -- Survey

This paper is a survey of methods for solving smooth (strongly) monotone stochastic variational inequalities. To begin with, we give the deterministic foundation from which the stochastic methods eventually evolved. Then we review methods for the general stochastic formulation, and look at the finite sum setup. The last parts of the paper are devoted to various recent (not necessarily stochastic) advances in algorithms for variational inequalities.

Accuracy guaranties for $\ell_1$ recovery of block-sparse signals

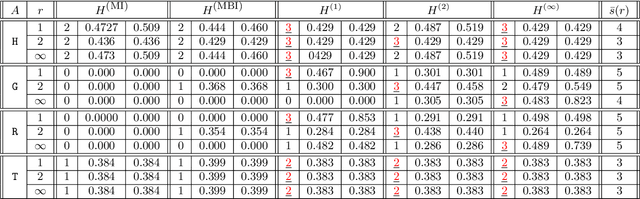
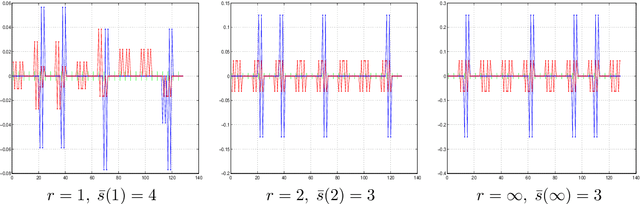
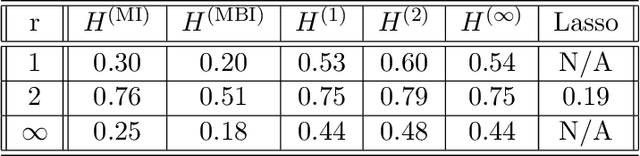
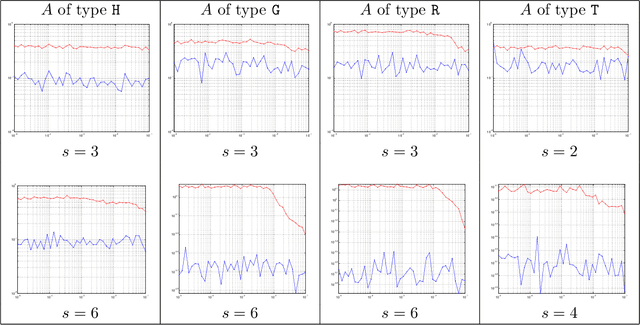
We introduce a general framework to handle structured models (sparse and block-sparse with possibly overlapping blocks). We discuss new methods for their recovery from incomplete observation, corrupted with deterministic and stochastic noise, using block-$\ell_1$ regularization. While the current theory provides promising bounds for the recovery errors under a number of different, yet mostly hard to verify conditions, our emphasis is on verifiable conditions on the problem parameters (sensing matrix and the block structure) which guarantee accurate recovery. Verifiability of our conditions not only leads to efficiently computable bounds for the recovery error but also allows us to optimize these error bounds with respect to the method parameters, and therefore construct estimators with improved statistical properties. To justify our approach, we also provide an oracle inequality, which links the properties of the proposed recovery algorithms and the best estimation performance. Furthermore, utilizing these verifiable conditions, we develop a computationally cheap alternative to block-$\ell_1$ minimization, the non-Euclidean Block Matching Pursuit algorithm. We close by presenting a numerical study to investigate the effect of different block regularizations and demonstrate the performance of the proposed recoveries.