Efficient Primal-Dual Algorithms for Large-Scale Multiclass Classification

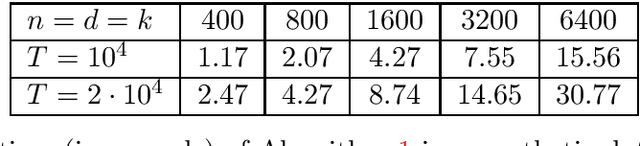
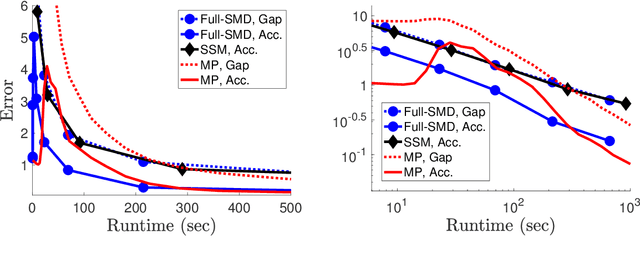
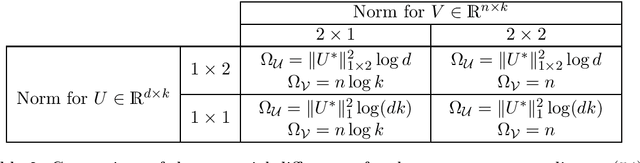
We develop efficient algorithms to train $\ell_1$-regularized linear classifiers with large dimensionality $d$ of the feature space, number of classes $k$, and sample size $n$. Our focus is on a special class of losses that includes, in particular, the multiclass hinge and logistic losses. Our approach combines several ideas: (i) passing to the equivalent saddle-point problem with a quasi-bilinear objective; (ii) applying stochastic mirror descent with a proper choice of geometry which guarantees a favorable accuracy bound; (iii) devising non-uniform sampling schemes to approximate the matrix products. In particular, for the multiclass hinge loss we propose a \textit{sublinear} algorithm with iterations performed in $O(d+n+k)$ arithmetic operations.

Affine Invariant Covariance Estimation for Heavy-Tailed Distributions

In this work we provide an estimator for the covariance matrix of a heavy-tailed random vector. We prove that the proposed estimator $\widehat{\mathbf{S}}$ admits \textit{affine-invariant} bounds of the form $$(1-\varepsilon) \mathbf{S} \preccurlyeq \widehat{\mathbf{S}} \preccurlyeq (1+\varepsilon) \mathbf{S}$$in high probability, where $\mathbf{S}$ is the unknown covariance matrix, and $\preccurlyeq$ is the positive semidefinite order on symmetric matrices. The result only requires the existence of fourth-order moments, and allows for $\varepsilon = O(\sqrt{\kappa^4 d/n})$ where $\kappa^4$ is some measure of kurtosis of the distribution, $d$ is the dimensionality of the space, and $n$ is the sample size. More generally, we can allow for regularization with level~$\lambda$, then $\varepsilon$ depends on the degrees of freedom number which is generally smaller than $d$. The computational cost of the proposed estimator is essentially~$O(d^2 n + d^3)$, comparable to the computational cost of the sample covariance matrix in the statistically interesting regime~$n \gg d$. Its applications to eigenvalue estimation with relative error and to ridge regression with heavy-tailed random design are discussed.

Beyond Least-Squares: Fast Rates for Regularized Empirical Risk Minimization through Self-Concordance

We consider learning methods based on the regularization of a convex empirical risk by a squared Hilbertian norm, a setting that includes linear predictors and non-linear predictors through positive-definite kernels. In order to go beyond the generic analysis leading to convergence rates of the excess risk as $O(1/\sqrt{n})$ from $n$ observations, we assume that the individual losses are self-concordant, that is, their third-order derivatives are bounded by their second-order derivatives. This setting includes least-squares, as well as all generalized linear models such as logistic and softmax regression. For this class of losses, we provide a bias-variance decomposition and show that the assumptions commonly made in least-squares regression, such as the source and capacity conditions, can be adapted to obtain fast non-asymptotic rates of convergence by improving the bias terms, the variance terms or both.

Finite-sample Analysis of M-estimators using Self-concordance

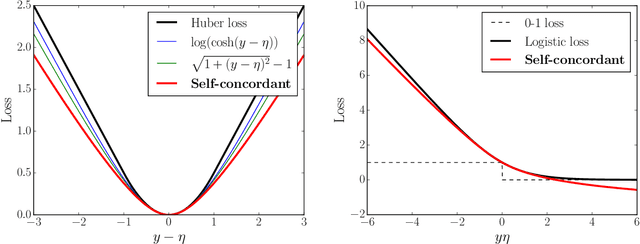
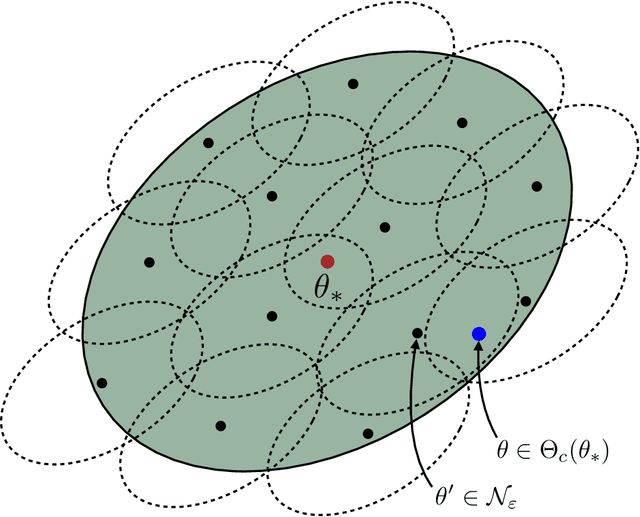
We demonstrate how self-concordance of the loss can be exploited to obtain asymptotically optimal rates for M-estimators in finite-sample regimes. We consider two classes of losses: (i) canonically self-concordant losses in the sense of Nesterov and Nemirovski (1994), i.e., with the third derivative bounded with the $3/2$ power of the second; (ii) pseudo self-concordant losses, for which the power is removed, as introduced by Bach (2010). These classes contain some losses arising in generalized linear models, including logistic regression; in addition, the second class includes some common pseudo-Huber losses. Our results consist in establishing the critical sample size sufficient to reach the asymptotically optimal excess risk for both classes of losses. Denoting $d$ the parameter dimension, and $d_{\text{eff}}$ the effective dimension which takes into account possible model misspecification, we find the critical sample size to be $O(d_{\text{eff}} \cdot d)$ for canonically self-concordant losses, and $O(\rho \cdot d_{\text{eff}} \cdot d)$ for pseudo self-concordant losses, where $\rho$ is the problem-dependent local curvature parameter. In contrast to the existing results, we only impose local assumptions on the data distribution, assuming that the calibrated design, i.e., the design scaled with the square root of the second derivative of the loss, is subgaussian at the best predictor $\theta_*$. Moreover, we obtain the improved bounds on the critical sample size, scaling near-linearly in $\max(d_{\text{eff}},d)$, under the extra assumption that the calibrated design is subgaussian in the Dikin ellipsoid of $\theta_*$. Motivated by these findings, we construct canonically self-concordant analogues of the Huber and logistic losses with improved statistical properties. Finally, we extend some of these results to $\ell_1$-regularized M-estimators in high dimensions.

Efficient First-Order Algorithms for Adaptive Signal Denoising

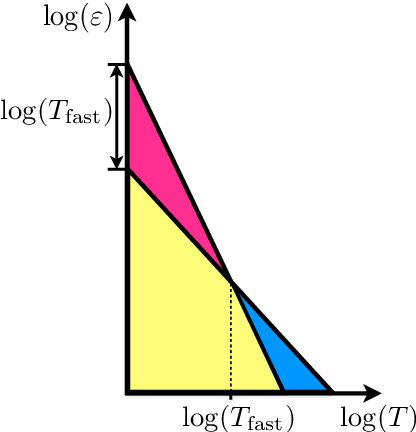
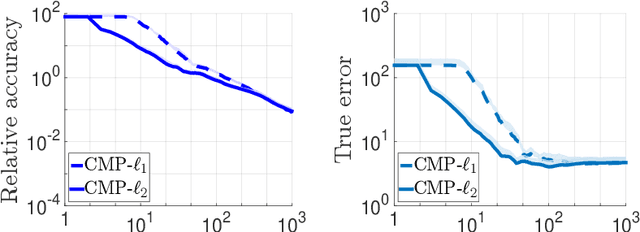
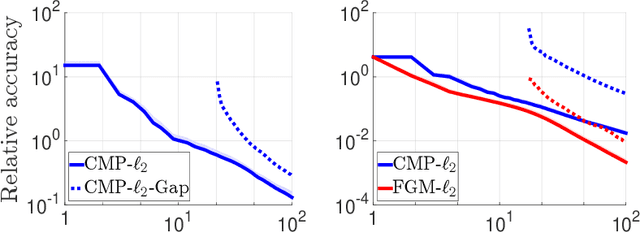
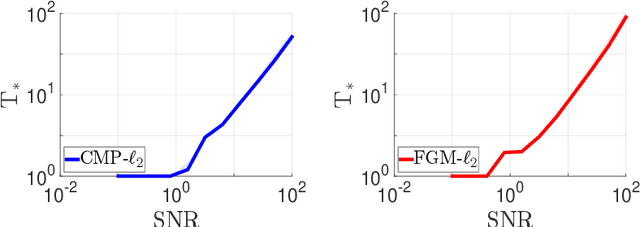
We consider the problem of discrete-time signal denoising, focusing on a specific family of non-linear convolution-type estimators. Each such estimator is associated with a time-invariant filter which is obtained adaptively, by solving a certain convex optimization problem. Adaptive convolution-type estimators were demonstrated to have favorable statistical properties. However, the question of their computational complexity remains largely unexplored, and in fact we are not aware of any publicly available implementation of these estimators. Our first contribution is an efficient implementation of these estimators via some known first-order proximal algorithms. Our second contribution is a computational complexity analysis of the proposed procedures, which takes into account their statistical nature and the related notion of statistical accuracy. The proposed procedures and their analysis are illustrated on a simulated data benchmark.

Adaptive Denoising of Signals with Shift-Invariant Structure

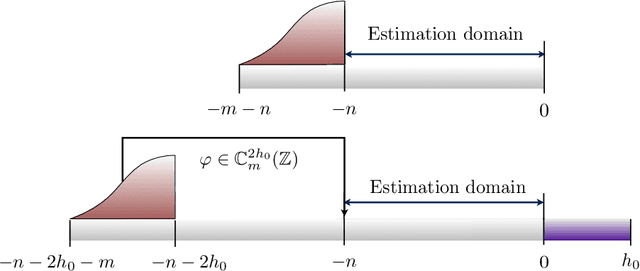
We study the problem of discrete-time signal denoising, following the line of research initiated by [Nem91] and further developed in [JN09, JN10, HJNO15, OHJN16]. Previous papers considered the following setup: the signal is assumed to admit a convolution-type linear oracle -- an unknown linear estimator in the form of the convolution of the observations with an unknown time-invariant filter with small $\ell_2$-norm. It was shown that such an oracle can be "mimicked" by an efficiently computable non-linear convolution-type estimator, in which the filter minimizes the Fourier-domain $\ell_\infty$-norm of the residual, regularized by the Fourier-domain $\ell_1$-norm of the filter. Following [OHJN16], here we study an alternative family of estimators, replacing the $\ell_\infty$-norm of the residual with the $\ell_2$-norm. Such estimators are found to have better statistical properties, in particular, we prove sharp oracle inequalities for their $\ell_2$-loss. Our guarantees require an extra assumption of approximate shift-invariance: the signal must be $\varkappa$-close, in $\ell_2$-metric, to some shift-invariant linear subspace with bounded dimension $s$. However, this subspace can be completely unknown, and the remainder terms in the oracle inequalities scale at most polynomially with $s$ and $\varkappa$. In conclusion, we show that the new assumption implies the previously considered one, providing explicit constructions of the convolution-type linear oracles with $\ell_2$-norm bounded in terms of parameters $s$ and $\varkappa$.