SRATTA : Sample Re-ATTribution Attack of Secure Aggregation in Federated Learning

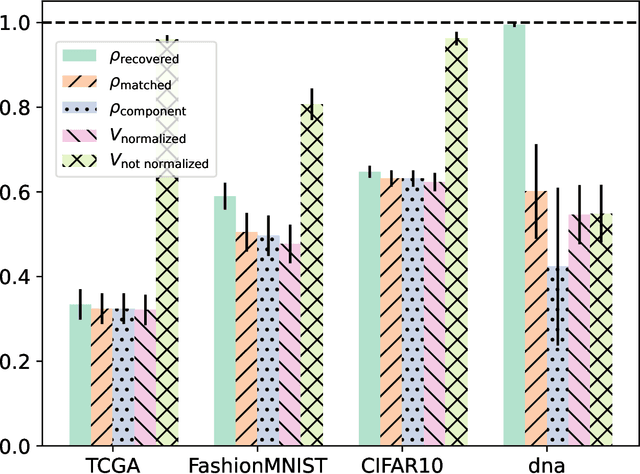
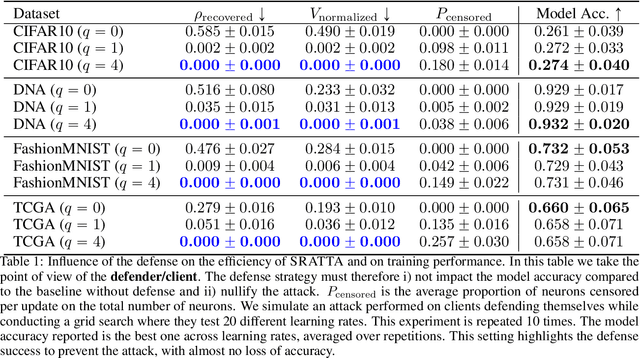
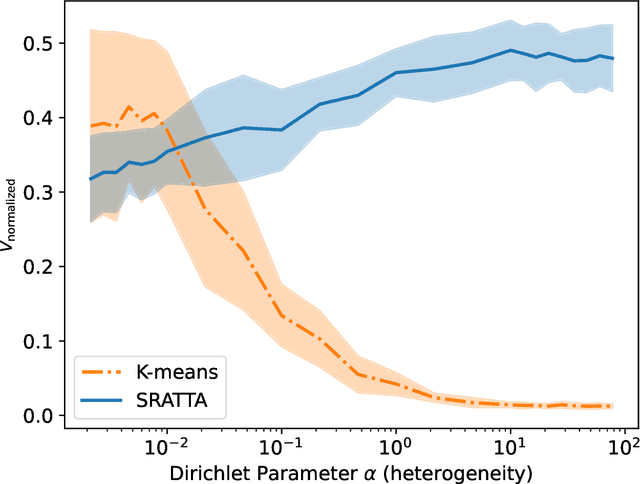
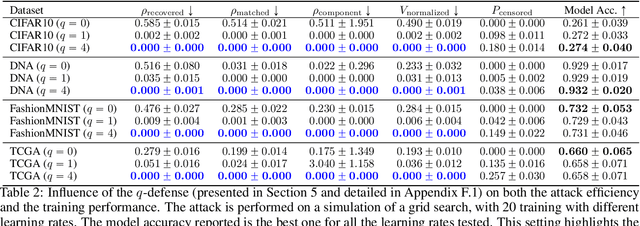
We consider a cross-silo federated learning (FL) setting where a machine learning model with a fully connected first layer is trained between different clients and a central server using FedAvg, and where the aggregation step can be performed with secure aggregation (SA). We present SRATTA an attack relying only on aggregated models which, under realistic assumptions, (i) recovers data samples from the different clients, and (ii) groups data samples coming from the same client together. While sample recovery has already been explored in an FL setting, the ability to group samples per client, despite the use of SA, is novel. This poses a significant unforeseen security threat to FL and effectively breaks SA. We show that SRATTA is both theoretically grounded and can be used in practice on realistic models and datasets. We also propose counter-measures, and claim that clients should play an active role to guarantee their privacy during training.

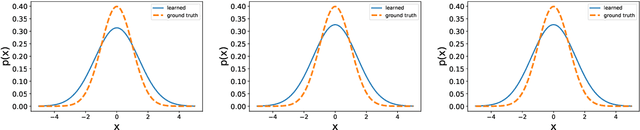
Sampling from Arbitrary Functions via PSD Models

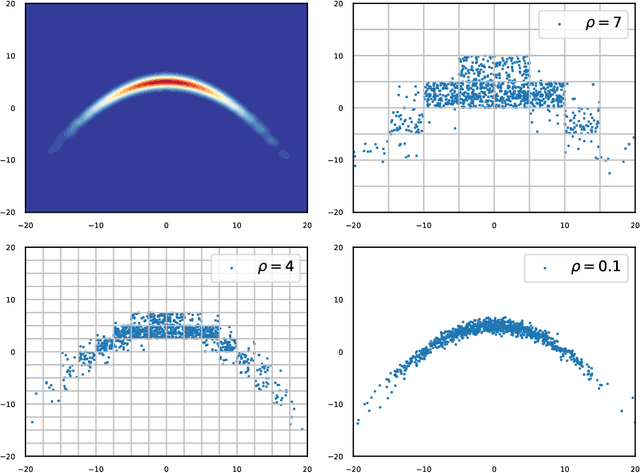
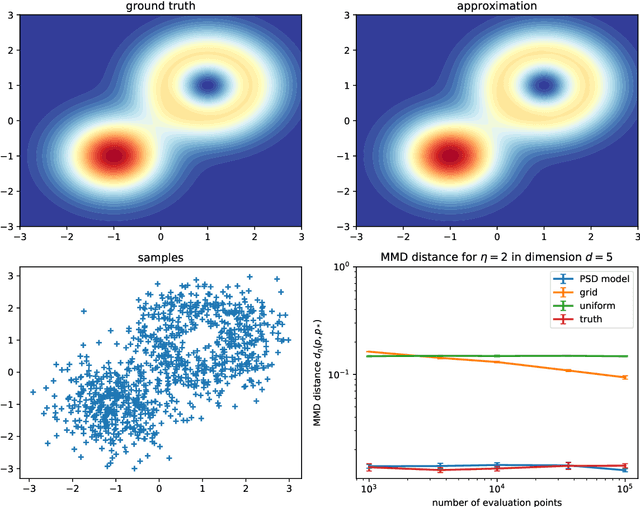
In many areas of applied statistics and machine learning, generating an arbitrary number of independent and identically distributed (i.i.d.) samples from a given distribution is a key task. When the distribution is known only through evaluations of the density, current methods either scale badly with the dimension or require very involved implementations. Instead, we take a two-step approach by first modeling the probability distribution and then sampling from that model. We use the recently introduced class of positive semi-definite (PSD) models, which have been shown to be efficient for approximating probability densities. We show that these models can approximate a large class of densities concisely using few evaluations, and present a simple algorithm to effectively sample from these models. We also present preliminary empirical results to illustrate our assertions.

Finding Global Minima via Kernel Approximations

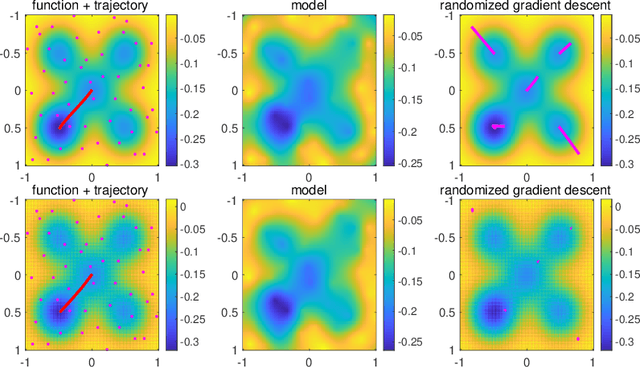
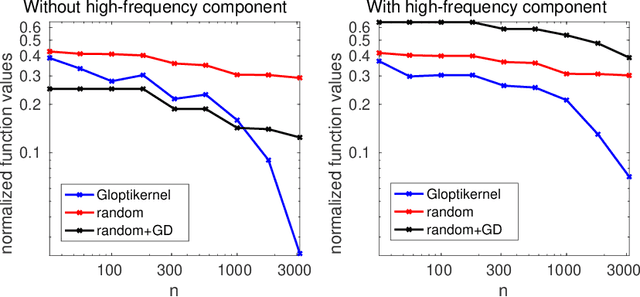
We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum. Given $n$ samples, the computational cost is $O(n^{3.5})$ in time, $O(n^2)$ in space, and we achieve a convergence rate to the global optimum that is $O(n^{-m/d + 1/2 + 3/d})$ where $m$ is the degree of differentiability of the function and $d$ the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions that have a large number of derivatives. Indeed, when $m$ is in the order of $d$, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst-case constants (that we track explicitly through the paper).

Non-parametric Models for Non-negative Functions

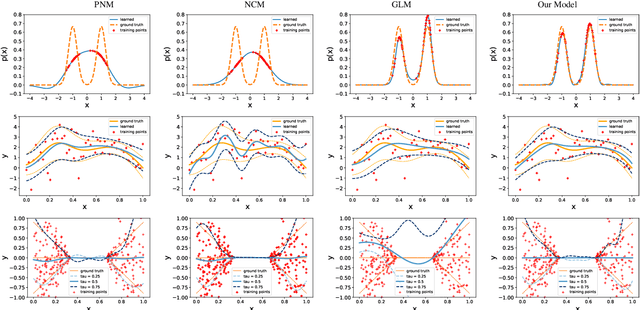
Linear models have shown great effectiveness and flexibility in many fields such as machine learning, signal processing and statistics. They can represent rich spaces of functions while preserving the convexity of the optimization problems where they are used, and are simple to evaluate, differentiate and integrate. However, for modeling non-negative functions, which are crucial for unsupervised learning, density estimation, or non-parametric Bayesian methods, linear models are not applicable directly. Moreover, current state-of-the-art models like generalized linear models either lead to non-convex optimization problems, or cannot be easily integrated. In this paper we provide the first model for non-negative functions which benefits from the same good properties of linear models. In particular, we prove that it admits a representer theorem and provide an efficient dual formulation for convex problems. We study its representation power, showing that the resulting space of functions is strictly richer than that of generalized linear models. Finally we extend the model and the theoretical results to functions with outputs in convex cones. The paper is complemented by an experimental evaluation of the model showing its effectiveness in terms of formulation, algorithmic derivation and practical results on the problems of density estimation, regression with heteroscedastic errors, and multiple quantile regression.

Globally Convergent Newton Methods for Ill-conditioned Generalized Self-concordant Losses

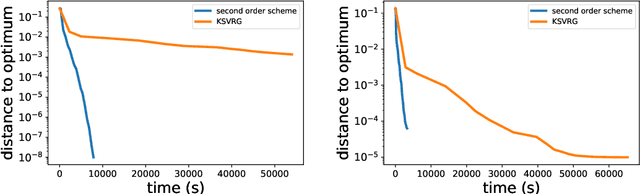
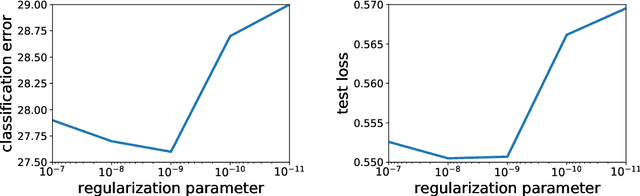
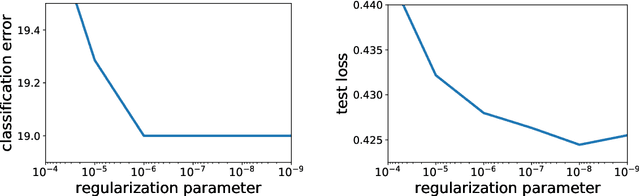
In this paper, we study large-scale convex optimization algorithms based on the Newton method applied to regularized generalized self-concordant losses, which include logistic regression and softmax regression. We first prove that our new simple scheme based on a sequence of problems with decreasing regularization parameters is provably globally convergent, that this convergence is linear with a constant factor which scales only logarithmically with the condition number. In the parametric setting, we obtain an algorithm with the same scaling than regular first-order methods but with an improved behavior, in particular in ill-conditioned problems. Second, in the non parametric machine learning setting, we provide an explicit algorithm combining the previous scheme with Nystr{\"o}m projection techniques, and prove that it achieves optimal generalization bounds with a time complexity of order O(ndf $\lambda$), a memory complexity of order O(df 2 $\lambda$) and no dependence on the condition number, generalizing the results known for least-squares regression. Here n is the number of observations and df $\lambda$ is the associated degrees of freedom. In particular, this is the first large-scale algorithm to solve logistic and softmax regressions in the non-parametric setting with large condition numbers and theoretical guarantees.

Beyond Least-Squares: Fast Rates for Regularized Empirical Risk Minimization through Self-Concordance

We consider learning methods based on the regularization of a convex empirical risk by a squared Hilbertian norm, a setting that includes linear predictors and non-linear predictors through positive-definite kernels. In order to go beyond the generic analysis leading to convergence rates of the excess risk as $O(1/\sqrt{n})$ from $n$ observations, we assume that the individual losses are self-concordant, that is, their third-order derivatives are bounded by their second-order derivatives. This setting includes least-squares, as well as all generalized linear models such as logistic and softmax regression. For this class of losses, we provide a bias-variance decomposition and show that the assumptions commonly made in least-squares regression, such as the source and capacity conditions, can be adapted to obtain fast non-asymptotic rates of convergence by improving the bias terms, the variance terms or both.