Globally Convergent Newton Methods for Ill-conditioned Generalized Self-concordant Losses
Paper and Code
Jul 03, 2019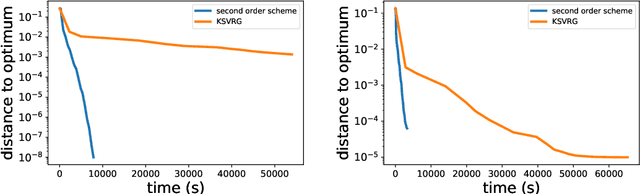

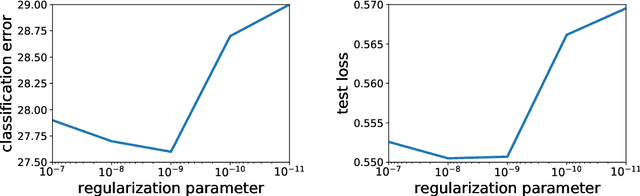
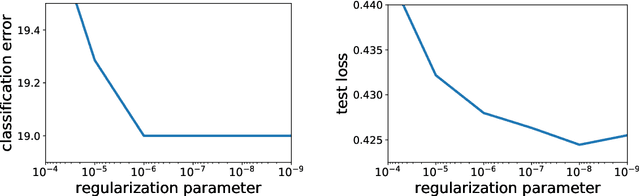
In this paper, we study large-scale convex optimization algorithms based on the Newton method applied to regularized generalized self-concordant losses, which include logistic regression and softmax regression. We first prove that our new simple scheme based on a sequence of problems with decreasing regularization parameters is provably globally convergent, that this convergence is linear with a constant factor which scales only logarithmically with the condition number. In the parametric setting, we obtain an algorithm with the same scaling than regular first-order methods but with an improved behavior, in particular in ill-conditioned problems. Second, in the non parametric machine learning setting, we provide an explicit algorithm combining the previous scheme with Nystr{\"o}m projection techniques, and prove that it achieves optimal generalization bounds with a time complexity of order O(ndf $\lambda$), a memory complexity of order O(df 2 $\lambda$) and no dependence on the condition number, generalizing the results known for least-squares regression. Here n is the number of observations and df $\lambda$ is the associated degrees of freedom. In particular, this is the first large-scale algorithm to solve logistic and softmax regressions in the non-parametric setting with large condition numbers and theoretical guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge