Finding Global Minima via Kernel Approximations
Paper and Code
Dec 22, 2020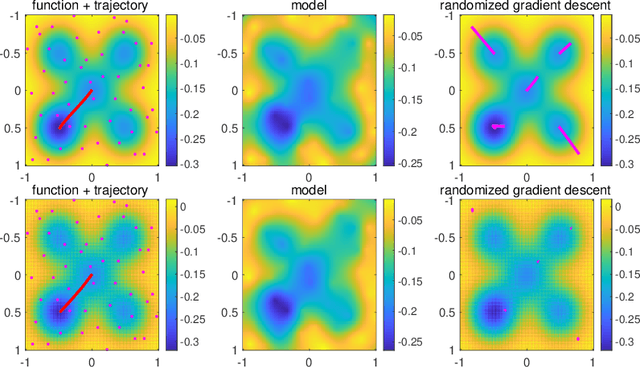
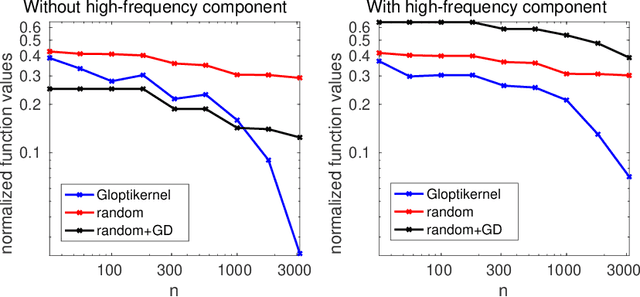
We consider the global minimization of smooth functions based solely on function evaluations. Algorithms that achieve the optimal number of function evaluations for a given precision level typically rely on explicitly constructing an approximation of the function which is then minimized with algorithms that have exponential running-time complexity. In this paper, we consider an approach that jointly models the function to approximate and finds a global minimum. This is done by using infinite sums of square smooth functions and has strong links with polynomial sum-of-squares hierarchies. Leveraging recent representation properties of reproducing kernel Hilbert spaces, the infinite-dimensional optimization problem can be solved by subsampling in time polynomial in the number of function evaluations, and with theoretical guarantees on the obtained minimum. Given $n$ samples, the computational cost is $O(n^{3.5})$ in time, $O(n^2)$ in space, and we achieve a convergence rate to the global optimum that is $O(n^{-m/d + 1/2 + 3/d})$ where $m$ is the degree of differentiability of the function and $d$ the number of dimensions. The rate is nearly optimal in the case of Sobolev functions and more generally makes the proposed method particularly suitable for functions that have a large number of derivatives. Indeed, when $m$ is in the order of $d$, the convergence rate to the global optimum does not suffer from the curse of dimensionality, which affects only the worst-case constants (that we track explicitly through the paper).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge