Finite-sample Analysis of M-estimators using Self-concordance

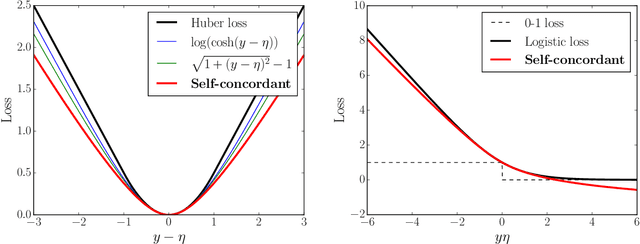
We demonstrate how self-concordance of the loss can be exploited to obtain asymptotically optimal rates for M-estimators in finite-sample regimes. We consider two classes of losses: (i) canonically self-concordant losses in the sense of Nesterov and Nemirovski (1994), i.e., with the third derivative bounded with the $3/2$ power of the second; (ii) pseudo self-concordant losses, for which the power is removed, as introduced by Bach (2010). These classes contain some losses arising in generalized linear models, including logistic regression; in addition, the second class includes some common pseudo-Huber losses. Our results consist in establishing the critical sample size sufficient to reach the asymptotically optimal excess risk for both classes of losses. Denoting $d$ the parameter dimension, and $d_{\text{eff}}$ the effective dimension which takes into account possible model misspecification, we find the critical sample size to be $O(d_{\text{eff}} \cdot d)$ for canonically self-concordant losses, and $O(\rho \cdot d_{\text{eff}} \cdot d)$ for pseudo self-concordant losses, where $\rho$ is the problem-dependent local curvature parameter. In contrast to the existing results, we only impose local assumptions on the data distribution, assuming that the calibrated design, i.e., the design scaled with the square root of the second derivative of the loss, is subgaussian at the best predictor $\theta_*$. Moreover, we obtain the improved bounds on the critical sample size, scaling near-linearly in $\max(d_{\text{eff}},d)$, under the extra assumption that the calibrated design is subgaussian in the Dikin ellipsoid of $\theta_*$. Motivated by these findings, we construct canonically self-concordant analogues of the Huber and logistic losses with improved statistical properties. Finally, we extend some of these results to $\ell_1$-regularized M-estimators in high dimensions.