Efficient Primal-Dual Algorithms for Large-Scale Multiclass Classification
Paper and Code
Feb 11, 2019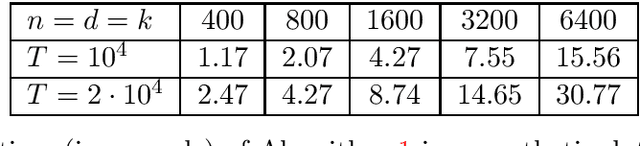
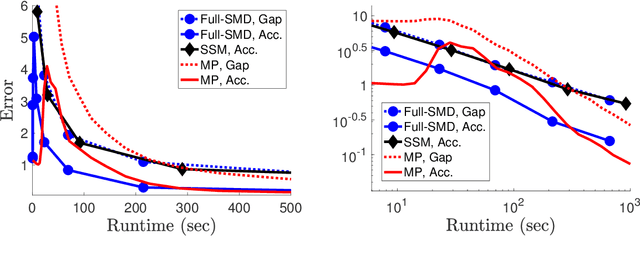
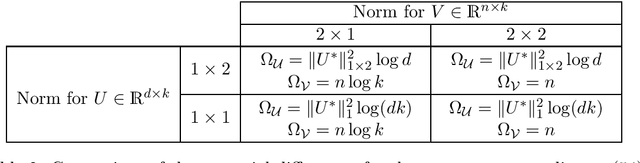
We develop efficient algorithms to train $\ell_1$-regularized linear classifiers with large dimensionality $d$ of the feature space, number of classes $k$, and sample size $n$. Our focus is on a special class of losses that includes, in particular, the multiclass hinge and logistic losses. Our approach combines several ideas: (i) passing to the equivalent saddle-point problem with a quasi-bilinear objective; (ii) applying stochastic mirror descent with a proper choice of geometry which guarantees a favorable accuracy bound; (iii) devising non-uniform sampling schemes to approximate the matrix products. In particular, for the multiclass hinge loss we propose a \textit{sublinear} algorithm with iterations performed in $O(d+n+k)$ arithmetic operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge