Efficient First-Order Algorithms for Adaptive Signal Denoising
Paper and Code
Jun 12, 2018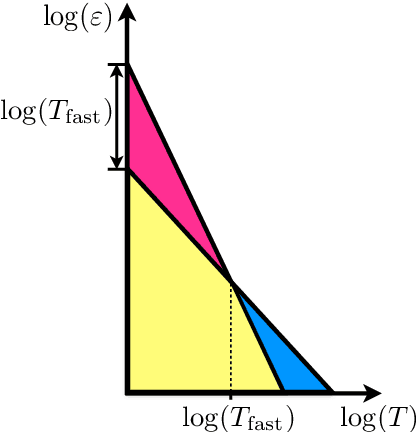
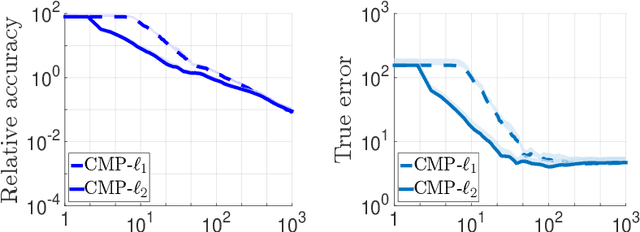
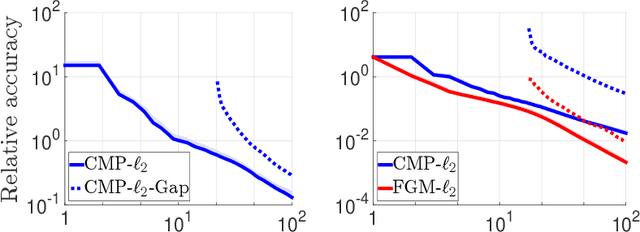
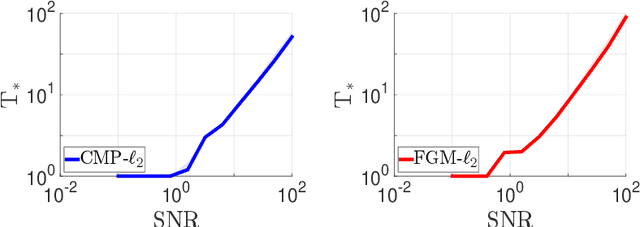
We consider the problem of discrete-time signal denoising, focusing on a specific family of non-linear convolution-type estimators. Each such estimator is associated with a time-invariant filter which is obtained adaptively, by solving a certain convex optimization problem. Adaptive convolution-type estimators were demonstrated to have favorable statistical properties. However, the question of their computational complexity remains largely unexplored, and in fact we are not aware of any publicly available implementation of these estimators. Our first contribution is an efficient implementation of these estimators via some known first-order proximal algorithms. Our second contribution is a computational complexity analysis of the proposed procedures, which takes into account their statistical nature and the related notion of statistical accuracy. The proposed procedures and their analysis are illustrated on a simulated data benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge