Conditional Gradient Algorithms for Norm-Regularized Smooth Convex Optimization
Paper and Code
Mar 28, 2013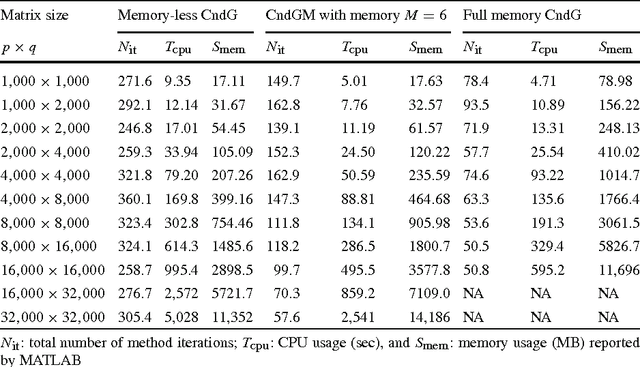
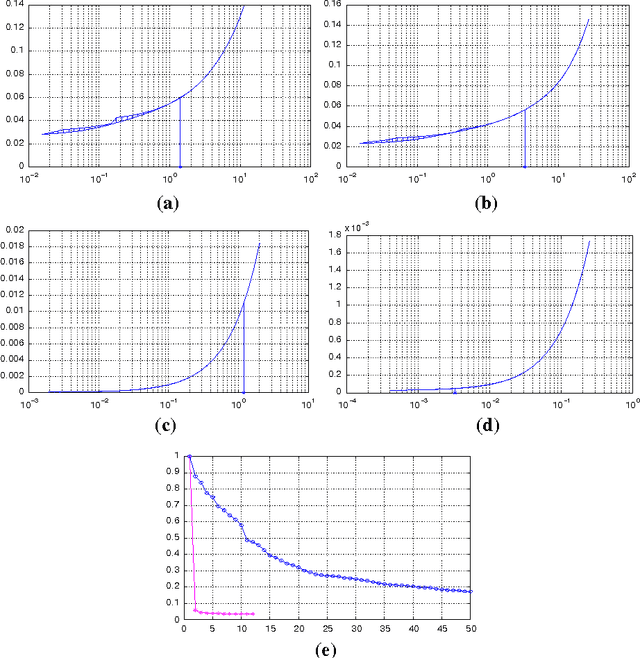
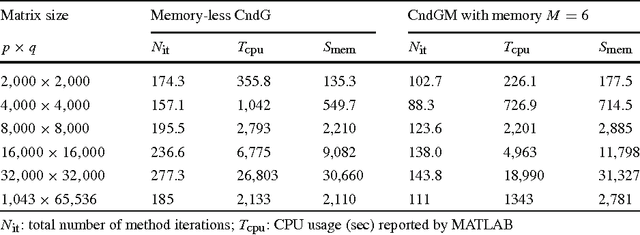

Motivated by some applications in signal processing and machine learning, we consider two convex optimization problems where, given a cone $K$, a norm $\|\cdot\|$ and a smooth convex function $f$, we want either 1) to minimize the norm over the intersection of the cone and a level set of $f$, or 2) to minimize over the cone the sum of $f$ and a multiple of the norm. We focus on the case where (a) the dimension of the problem is too large to allow for interior point algorithms, (b) $\|\cdot\|$ is "too complicated" to allow for computationally cheap Bregman projections required in the first-order proximal gradient algorithms. On the other hand, we assume that {it is relatively easy to minimize linear forms over the intersection of $K$ and the unit $\|\cdot\|$-ball}. Motivating examples are given by the nuclear norm with $K$ being the entire space of matrices, or the positive semidefinite cone in the space of symmetric matrices, and the Total Variation norm on the space of 2D images. We discuss versions of the Conditional Gradient algorithm capable to handle our problems of interest, provide the related theoretical efficiency estimates and outline some applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge