On robust recovery of signals from indirect observations

We consider an uncertain linear inverse problem as follows. Given observation $\omega=Ax_*+\zeta$ where $A\in {\bf R}^{m\times p}$ and $\zeta\in {\bf R}^{m}$ is observation noise, we want to recover unknown signal $x_*$, known to belong to a convex set ${\cal X}\subset{\bf R}^{n}$. As opposed to the "standard" setting of such problem, we suppose that the model noise $\zeta$ is "corrupted" -- contains an uncertain (deterministic dense or singular) component. Specifically, we assume that $\zeta$ decomposes into $\zeta=N\nu_*+\xi$ where $\xi$ is the random noise and $N\nu_*$ is the "adversarial contamination" with known $\cal N\subset {\bf R}^n$ such that $\nu_*\in \cal N$ and $N\in {\bf R}^{m\times n}$. We consider two "uncertainty setups" in which $\cal N$ is either a convex bounded set or is the set of sparse vectors (with at most $s$ nonvanishing entries). We analyse the performance of "uncertainty-immunized" polyhedral estimates -- a particular class of nonlinear estimates as introduced in [15, 16] -- and show how "presumably good" estimates of the sort may be constructed in the situation where the signal set is an ellitope (essentially, a symmetric convex set delimited by quadratic surfaces) by means of efficient convex optimization routines.

Stochastic Mirror Descent for Large-Scale Sparse Recovery

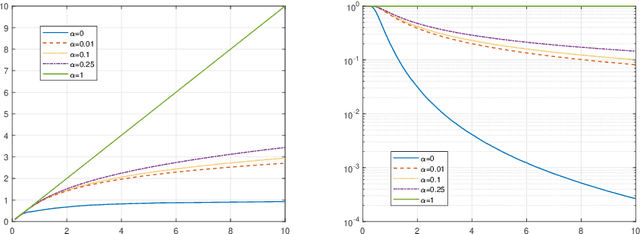
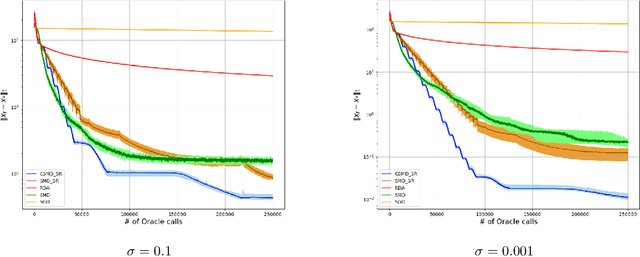
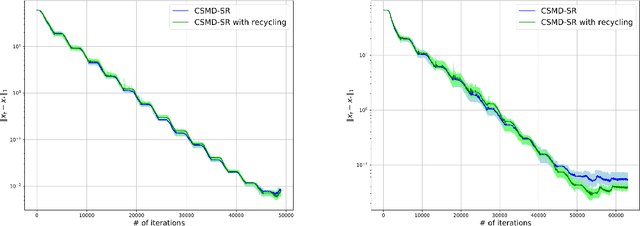
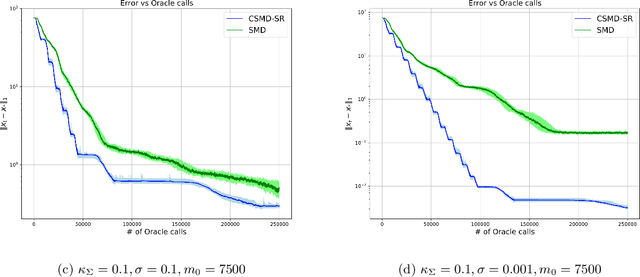
In this paper we discuss an application of Stochastic Approximation to statistical estimation of high-dimensional sparse parameters. The proposed solution reduces to resolving a penalized stochastic optimization problem on each stage of a multistage algorithm; each problem being solved to a prescribed accuracy by the non-Euclidean Composite Stochastic Mirror Descent (CSMD) algorithm. Assuming that the problem objective is smooth and quadratically minorated and stochastic perturbations are sub-Gaussian, our analysis prescribes the method parameters which ensure fast convergence of the estimation error (the radius of a confidence ball of a given norm around the approximate solution). This convergence is linear during the first "preliminary" phase of the routine and is sublinear during the second "asymptotic" phase. We consider an application of the proposed approach to sparse Generalized Linear Regression problem. In this setting, we show that the proposed algorithm attains the optimal convergence of the estimation error under weak assumptions on the regressor distribution. We also present a numerical study illustrating the performance of the algorithm on high-dimensional simulation data.