On unified view of nullspace-type conditions for recoveries associated with general sparsity structures
Paper and Code
Jul 04, 2012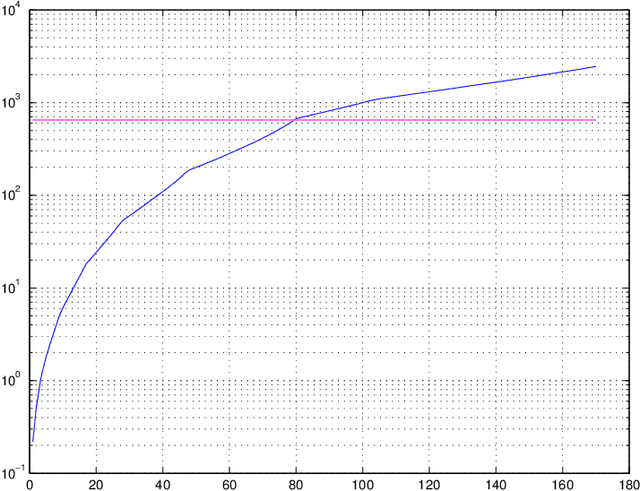
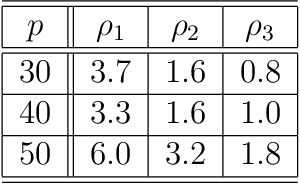
We discuss a general notion of "sparsity structure" and associated recoveries of a sparse signal from its linear image of reduced dimension possibly corrupted with noise. Our approach allows for unified treatment of (a) the "usual sparsity" and "usual $\ell_1$ recovery," (b) block-sparsity with possibly overlapping blocks and associated block-$\ell_1$ recovery, and (c) low-rank-oriented recovery by nuclear norm minimization. The proposed recovery routines are natural extensions of the usual $\ell_1$ minimization used in Compressed Sensing. Specifically we present nullspace-type sufficient conditions for the recovery to be precise on sparse signals in the noiseless case. Then we derive error bounds for imperfect (nearly sparse signal, presence of observation noise, etc.) recovery under these conditions. In all of these cases, we present efficiently verifiable sufficient conditions for the validity of the associated nullspace properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge