Adaptive Nonparametric Clustering
Paper and Code
Sep 26, 2017
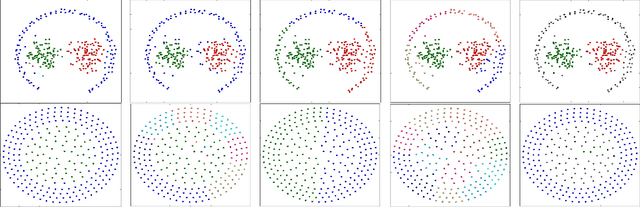
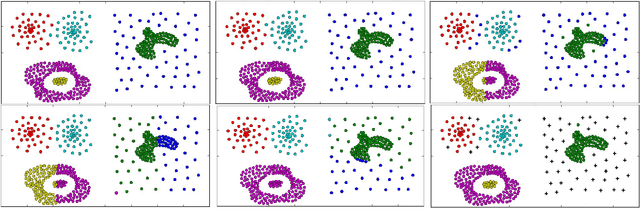
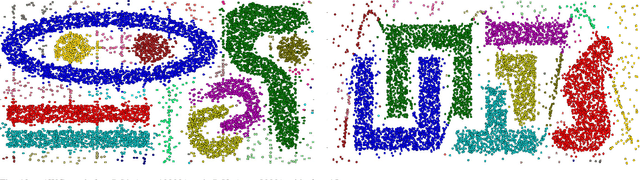
This paper presents a new approach to non-parametric cluster analysis called Adaptive Weights Clustering (AWC). The idea is to identify the clustering structure by checking at different points and for different scales on departure from local homogeneity. The proposed procedure describes the clustering structure in terms of weights \( w_{ij} \) each of them measures the degree of local inhomogeneity for two neighbor local clusters using statistical tests of "no gap" between them. % The procedure starts from very local scale, then the parameter of locality grows by some factor at each step. The method is fully adaptive and does not require to specify the number of clusters or their structure. The clustering results are not sensitive to noise and outliers, the procedure is able to recover different clusters with sharp edges or manifold structure. The method is scalable and computationally feasible. An intensive numerical study shows a state-of-the-art performance of the method in various artificial examples and applications to text data. Our theoretical study states optimal sensitivity of AWC to local inhomogeneity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge