Critical Points and Convergence Analysis of Generative Deep Linear Networks Trained with Bures-Wasserstein Loss

We consider a deep matrix factorization model of covariance matrices trained with the Bures-Wasserstein distance. While recent works have made important advances in the study of the optimization problem for overparametrized low-rank matrix approximation, much emphasis has been placed on discriminative settings and the square loss. In contrast, our model considers another interesting type of loss and connects with the generative setting. We characterize the critical points and minimizers of the Bures-Wasserstein distance over the space of rank-bounded matrices. For low-rank matrices the Hessian of this loss can theoretically blow up, which creates challenges to analyze convergence of optimizaton methods. We establish convergence results for gradient flow using a smooth perturbative version of the loss and convergence results for finite step size gradient descent under certain assumptions on the initial weights.

High dimensional change-point detection: a complete graph approach

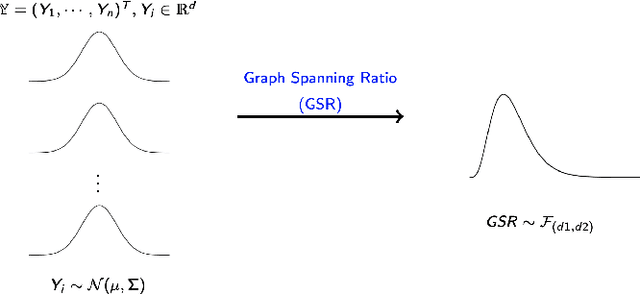
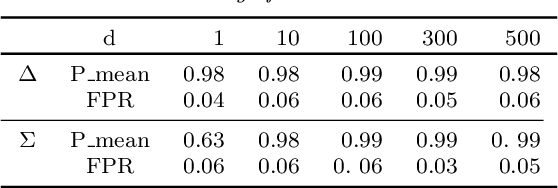
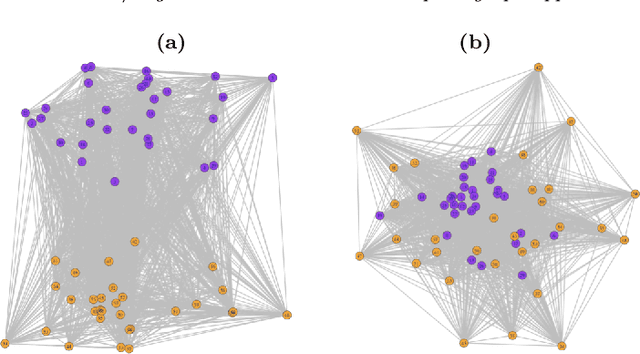
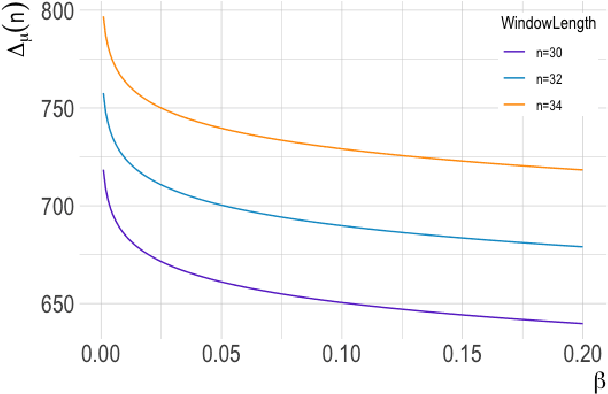
The aim of online change-point detection is for a accurate, timely discovery of structural breaks. As data dimension outgrows the number of data in observation, online detection becomes challenging. Existing methods typically test only the change of mean, which omit the practical aspect of change of variance. We propose a complete graph-based, change-point detection algorithm to detect change of mean and variance from low to high-dimensional online data with a variable scanning window. Inspired by complete graph structure, we introduce graph-spanning ratios to map high-dimensional data into metrics, and then test statistically if a change of mean or change of variance occurs. Theoretical study shows that our approach has the desirable pivotal property and is powerful with prescribed error probabilities. We demonstrate that this framework outperforms other methods in terms of detection power. Our approach has high detection power with small and multiple scanning window, which allows timely detection of change-point in the online setting. Finally, we applied the method to financial data to detect change-points in S&P 500 stocks.

Online Graph-Based Change-Point Detection for High Dimensional Data

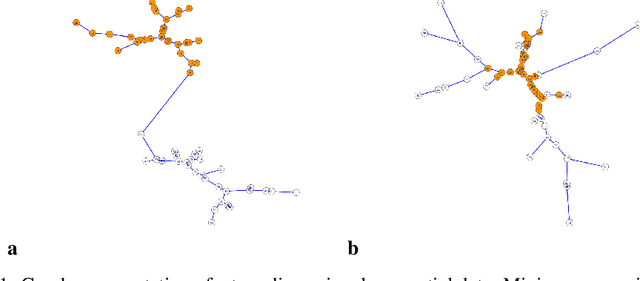
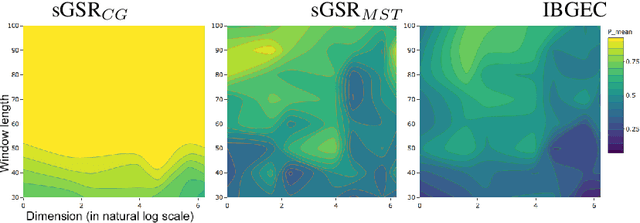
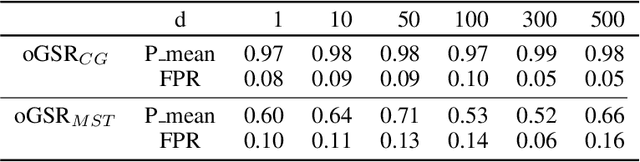
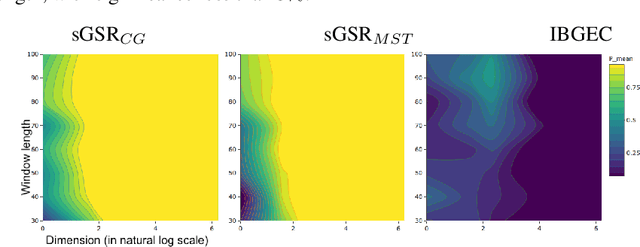
Online change-point detection (OCPD) is important for application in various areas such as finance, biology, and the Internet of Things (IoT). However, OCPD faces major challenges due to high-dimensionality, and it is still rarely studied in literature. In this paper, we propose a novel, online, graph-based, change-point detection algorithm to detect change of distribution in low- to high-dimensional data. We introduce a similarity measure, which is derived from the graph-spanning ratio, to test statistically if a change occurs. Through numerical study using artificial online datasets, our data-driven approach demonstrates high detection power for high-dimensional data, while the false alarm rate (type I error) is controlled at a nominal significant level. In particular, our graph-spanning approach has desirable power with small and multiple scanning window, which allows timely detection of change-point in the online setting.