Convergence of stochastic gradient descent under a local Lajasiewicz condition for deep neural networks

We extend the global convergence result of Chatterjee \cite{chatterjee2022convergence} by considering the stochastic gradient descent (SGD) for non-convex objective functions. With minimal additional assumptions that can be realized by finitely wide neural networks, we prove that if we initialize inside a local region where the \L{}ajasiewicz condition holds, with a positive probability, the stochastic gradient iterates converge to a global minimum inside this region. A key component of our proof is to ensure that the whole trajectories of SGD stay inside the local region with a positive probability. For that, we assume the SGD noise scales with the objective function, which is called machine learning noise and achievable in many real examples. Furthermore, we provide a negative argument to show why using the boundedness of noise with Robbins-Monro type step sizes is not enough to keep the key component valid.

Critical Points and Convergence Analysis of Generative Deep Linear Networks Trained with Bures-Wasserstein Loss

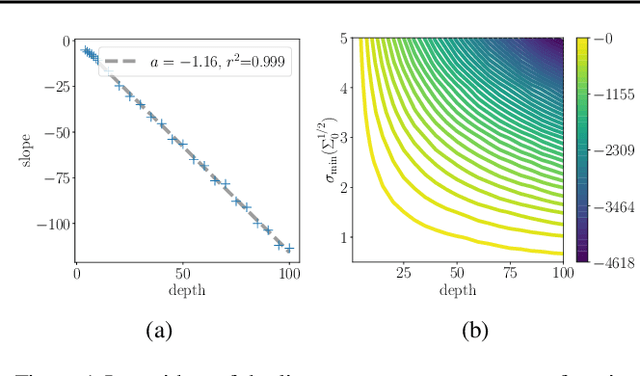
We consider a deep matrix factorization model of covariance matrices trained with the Bures-Wasserstein distance. While recent works have made important advances in the study of the optimization problem for overparametrized low-rank matrix approximation, much emphasis has been placed on discriminative settings and the square loss. In contrast, our model considers another interesting type of loss and connects with the generative setting. We characterize the critical points and minimizers of the Bures-Wasserstein distance over the space of rank-bounded matrices. For low-rank matrices the Hessian of this loss can theoretically blow up, which creates challenges to analyze convergence of optimizaton methods. We establish convergence results for gradient flow using a smooth perturbative version of the loss and convergence results for finite step size gradient descent under certain assumptions on the initial weights.

Combining resampling and reweighting for faithful stochastic optimization

Many machine learning and data science tasks require solving non-convex optimization problems. When the loss function is a sum of multiple terms, a popular method is stochastic gradient descent. Viewed as a process for sampling the loss function landscape, the stochastic gradient descent is known to prefer flat local minimums. Though this is desired for certain optimization problems such as in deep learning, it causes issues when the goal is to find the global minimum, especially if the global minimum resides in a sharp valley. Illustrated with a simple motivating example, we show that the fundamental reason is that the difference in the Lipschitz constants of multiple terms in the loss function causes stochastic gradient descent to experience different variances at different minimums. In order to mitigate this effect and perform faithful optimization, we propose a combined resampling-reweighting scheme to balance the variance at local minimums and extend to general loss functions. We also explain from the stochastic asymptotics perspective how the proposed scheme is more likely to select the true global minimum when compared with the vanilla stochastic gradient descent. Experiments from robust statistics, computational chemistry, and neural network training are provided to demonstrate the theoretical findings.

Hierarchical RNNs-Based Transformers MADDPG for Mixed Cooperative-Competitive Environments

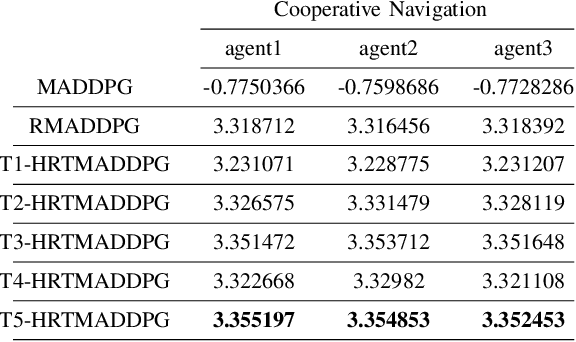
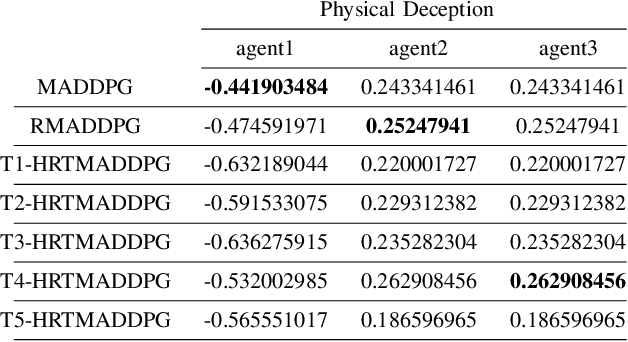
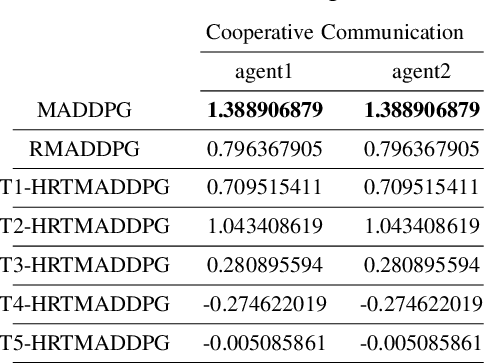
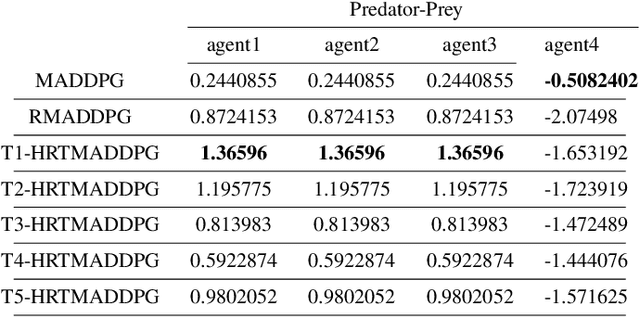
At present, attention mechanism has been widely applied to the fields of deep learning models. Structural models that based on attention mechanism can not only record the relationships between features position, but also can measure the importance of different features based on their weights. By establishing dynamically weighted parameters for choosing relevant and irrelevant features, the key information can be strengthened, and the irrelevant information can be weakened. Therefore, the efficiency of deep learning algorithms can be significantly elevated and improved. Although transformers have been performed very well in many fields including reinforcement learning, there are still many problems and applications can be solved and made with transformers within this area. MARL (known as Multi-Agent Reinforcement Learning) can be recognized as a set of independent agents trying to adapt and learn through their way to reach the goal. In order to emphasize the relationship between each MDP decision in a certain time period, we applied the hierarchical coding method and validated the effectiveness of this method. This paper proposed a hierarchical transformers MADDPG based on RNN which we call it Hierarchical RNNs-Based Transformers MADDPG(HRTMADDPG). It consists of a lower level encoder based on RNNs that encodes multiple step sizes in each time sequence, and it also consists of an upper sequence level encoder based on transformer for learning the correlations between multiple sequences so that we can capture the causal relationship between sub-time sequences and make HRTMADDPG more efficient.

Why resampling outperforms reweighting for correcting sampling bias

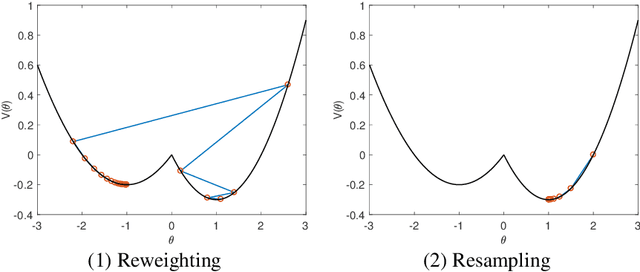
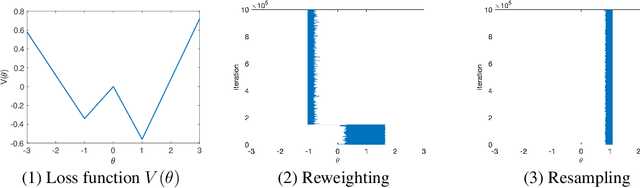
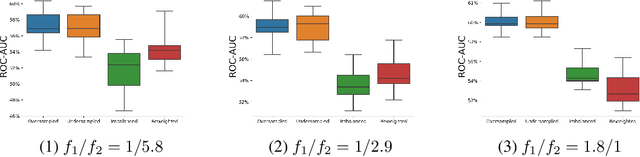
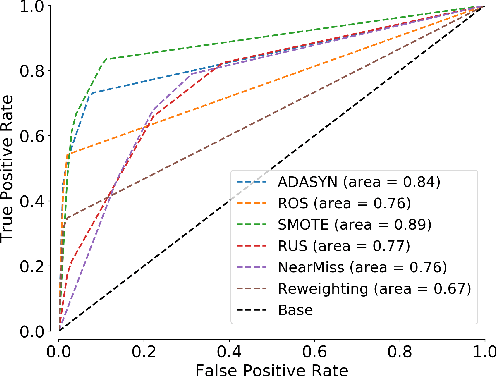
A data set sampled from a certain population is biased if the subgroups of the population are sampled at proportions that are significantly different from their underlying proportions. Training machine learning models on biased data sets requires correction techniques to compensate for potential biases. We consider two commonly-used techniques, resampling and reweighting, that rebalance the proportions of the subgroups to maintain the desired objective function. Though statistically equivalent, it has been observed that reweighting outperforms resampling when combined with stochastic gradient algorithms. By analyzing illustrative examples, we explain the reason behind this phenomenon using tools from dynamical stability and stochastic asymptotics. We also present experiments from regression, classification, and off-policy prediction to demonstrate that this is a general phenomenon. We argue that it is imperative to consider the objective function design and the optimization algorithm together while addressing the sampling bias.

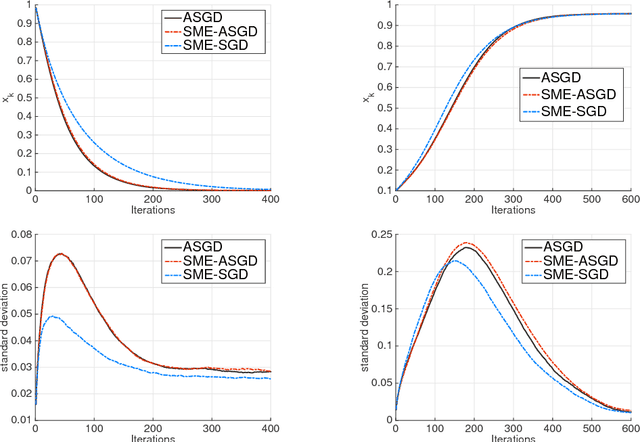
Stochastic modified equations for the asynchronous stochastic gradient descent

We propose a stochastic modified equations (SME) for modeling the asynchronous stochastic gradient descent (ASGD) algorithms. The resulting SME of Langevin type extracts more information about the ASGD dynamics and elucidates the relationship between different types of stochastic gradient algorithms. We show the convergence of ASGD to the SME in the continuous time limit, as well as the SME's precise prediction to the trajectories of ASGD with various forcing terms. As an application of the SME, we propose an optimal mini-batching strategy for ASGD via solving the optimal control problem of the associated SME.