High dimensional change-point detection: a complete graph approach

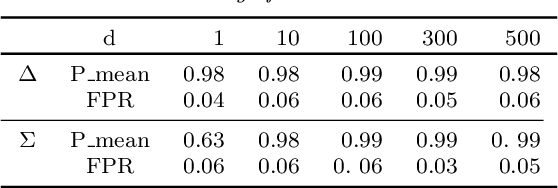
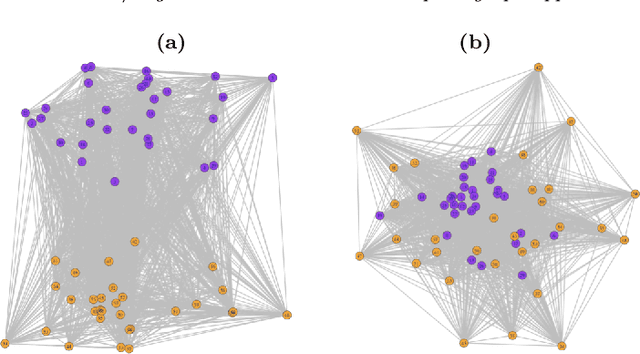
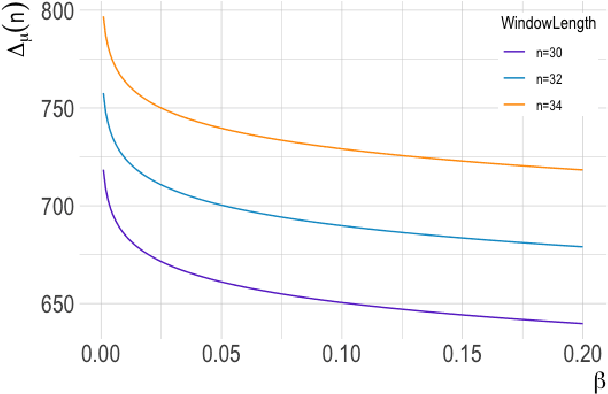
The aim of online change-point detection is for a accurate, timely discovery of structural breaks. As data dimension outgrows the number of data in observation, online detection becomes challenging. Existing methods typically test only the change of mean, which omit the practical aspect of change of variance. We propose a complete graph-based, change-point detection algorithm to detect change of mean and variance from low to high-dimensional online data with a variable scanning window. Inspired by complete graph structure, we introduce graph-spanning ratios to map high-dimensional data into metrics, and then test statistically if a change of mean or change of variance occurs. Theoretical study shows that our approach has the desirable pivotal property and is powerful with prescribed error probabilities. We demonstrate that this framework outperforms other methods in terms of detection power. Our approach has high detection power with small and multiple scanning window, which allows timely detection of change-point in the online setting. Finally, we applied the method to financial data to detect change-points in S&P 500 stocks.