An Interactive Interface for Novel Class Discovery in Tabular Data

Novel Class Discovery (NCD) is the problem of trying to discover novel classes in an unlabeled set, given a labeled set of different but related classes. The majority of NCD methods proposed so far only deal with image data, despite tabular data being among the most widely used type of data in practical applications. To interpret the results of clustering or NCD algorithms, data scientists need to understand the domain- and application-specific attributes of tabular data. This task is difficult and can often only be performed by a domain expert. Therefore, this interface allows a domain expert to easily run state-of-the-art algorithms for NCD in tabular data. With minimal knowledge in data science, interpretable results can be generated.

Novel Class Discovery: an Introduction and Key Concepts

Novel Class Discovery (NCD) is a growing field where we are given during training a labeled set of known classes and an unlabeled set of different classes that must be discovered. In recent years, many methods have been proposed to address this problem, and the field has begun to mature. In this paper, we provide a comprehensive survey of the state-of-the-art NCD methods. We start by formally defining the NCD problem and introducing important notions. We then give an overview of the different families of approaches, organized by the way they transfer knowledge from the labeled set to the unlabeled set. We find that they either learn in two stages, by first extracting knowledge from the labeled data only and then applying it to the unlabeled data, or in one stage by conjointly learning on both sets. For each family, we describe their general principle and detail a few representative methods. Then, we briefly introduce some new related tasks inspired by the increasing number of NCD works. We also present some common tools and techniques used in NCD, such as pseudo labeling, self-supervised learning and contrastive learning. Finally, to help readers unfamiliar with the NCD problem differentiate it from other closely related domains, we summarize some of the closest areas of research and discuss their main differences.

Découvrir de nouvelles classes dans des données tabulaires

In Novel Class Discovery (NCD), the goal is to find new classes in an unlabeled set given a labeled set of known but different classes. While NCD has recently gained attention from the community, no framework has yet been proposed for heterogeneous tabular data, despite being a very common representation of data. In this paper, we propose TabularNCD, a new method for discovering novel classes in tabular data. We show a way to extract knowledge from already known classes to guide the discovery process of novel classes in the context of tabular data which contains heterogeneous variables. A part of this process is done by a new method for defining pseudo labels, and we follow recent findings in Multi-Task Learning to optimize a joint objective function. Our method demonstrates that NCD is not only applicable to images but also to heterogeneous tabular data.

A Method for Discovering Novel Classes in Tabular Data

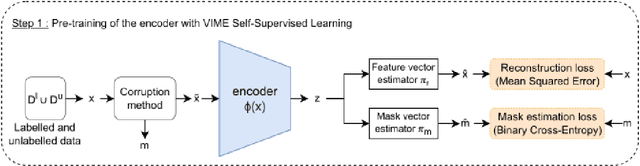
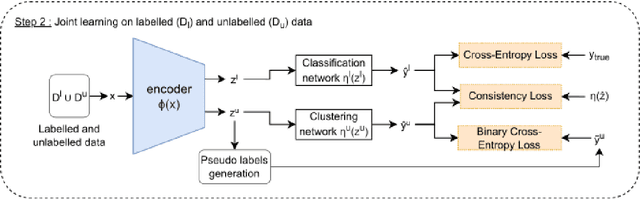
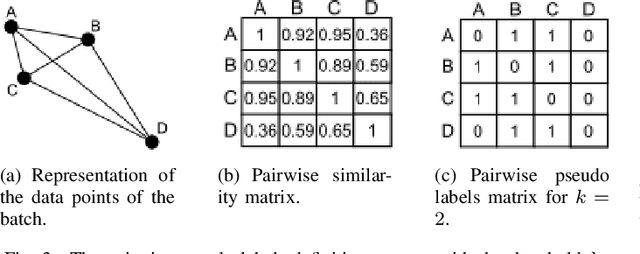
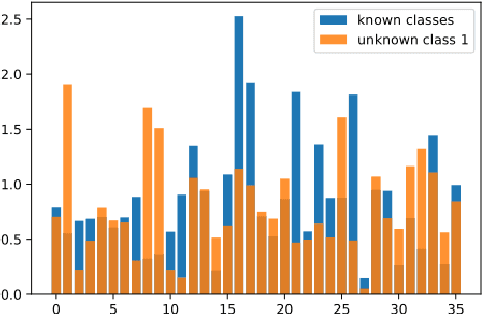
In Novel Class Discovery (NCD), the goal is to find new classes in an unlabeled set given a labeled set of known but different classes. While NCD has recently gained attention from the community, no framework has yet been proposed for heterogeneous tabular data, despite being a very common representation of data. In this paper, we propose TabularNCD, a new method for discovering novel classes in tabular data. We show a way to extract knowledge from already known classes to guide the discovery process of novel classes in the context of tabular data which contains heterogeneous variables. A part of this process is done by a new method for defining pseudo labels, and we follow recent findings in Multi-Task Learning to optimize a joint objective function. Our method demonstrates that NCD is not only applicable to images but also to heterogeneous tabular data. Extensive experiments are conducted to evaluate our method and demonstrate its effectiveness against 3 competitors on 7 diverse public classification datasets.

On the Variational Posterior of Dirichlet Process Deep Latent Gaussian Mixture Models

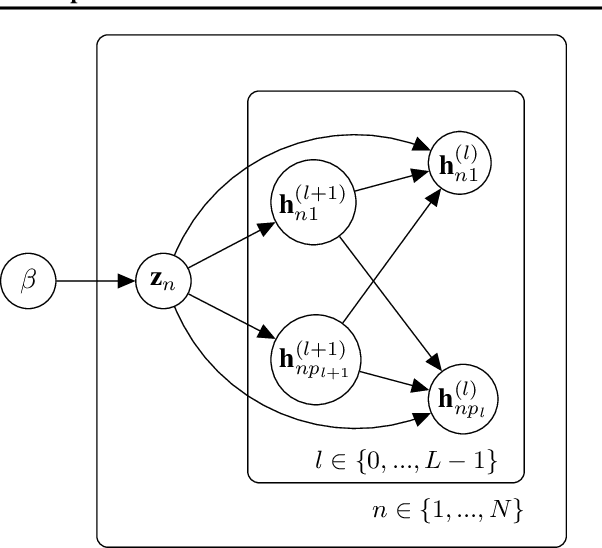
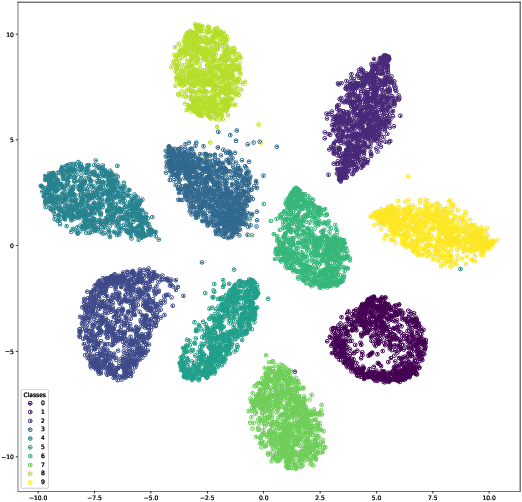
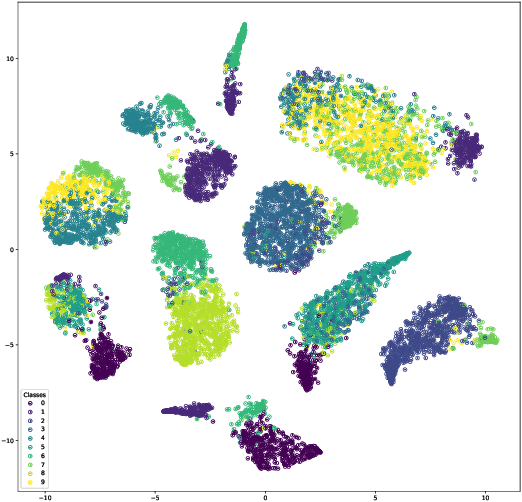
Thanks to the reparameterization trick, deep latent Gaussian models have shown tremendous success recently in learning latent representations. The ability to couple them however with nonparamet-ric priors such as the Dirichlet Process (DP) hasn't seen similar success due to its non parameteriz-able nature. In this paper, we present an alternative treatment of the variational posterior of the Dirichlet Process Deep Latent Gaussian Mixture Model (DP-DLGMM), where we show that the prior cluster parameters and the variational posteriors of the beta distributions and cluster hidden variables can be updated in closed-form. This leads to a standard reparameterization trick on the Gaussian latent variables knowing the cluster assignments. We demonstrate our approach on standard benchmark datasets, we show that our model is capable of generating realistic samples for each cluster obtained, and manifests competitive performance in a semi-supervised setting.