MultiHU-TD: Multifeature Hyperspectral Unmixing Based on Tensor Decomposition

Hyperspectral unmixing allows representing mixed pixels as a set of pure materials weighted by their abundances. Spectral features alone are often insufficient, so it is common to rely on other features of the scene. Matrix models become insufficient when the hyperspectral image (HSI) is represented as a high-order tensor with additional features in a multimodal, multifeature framework. Tensor models such as canonical polyadic decomposition allow for this kind of unmixing but lack a general framework and interpretability of the results. In this article, we propose an interpretable methodological framework for low-rank multifeature hyperspectral unmixing based on tensor decomposition (MultiHU-TD) that incorporates the abundance sum-to-one constraint in the alternating optimization alternating direction method of multipliers (ADMM) algorithm and provide in-depth mathematical, physical, and graphical interpretation and connections with the extended linear mixing model. As additional features, we propose to incorporate mathematical morphology and reframe a previous work on neighborhood patches within MultiHU-TD. Experiments on real HSIs showcase the interpretability of the model and the analysis of the results. Python and MATLAB implementations are made available on GitHub.

Joint Normality Test Via Two-Dimensional Projection

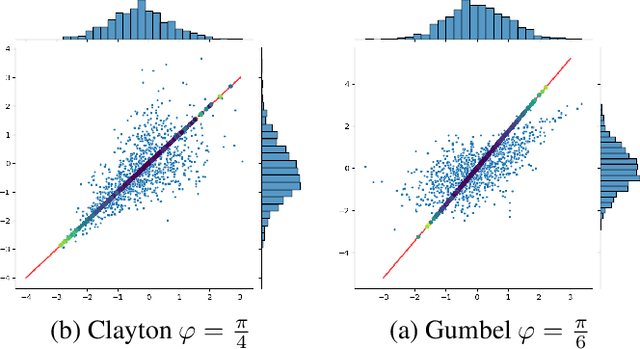
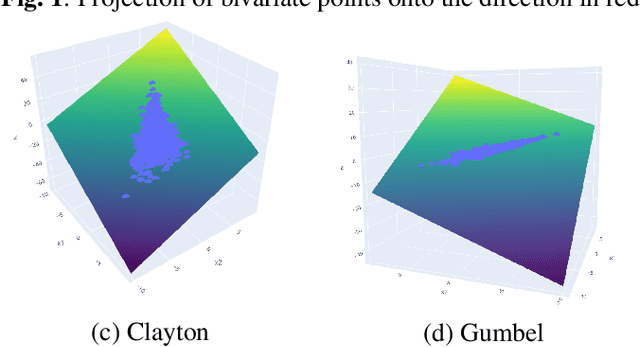
Extensive literature exists on how to test for normality, especially for identically and independently distributed (i.i.d) processes. The case of dependent samples has also been addressed, but only for scalar random processes. For this reason, we have proposed a joint normality test for multivariate time-series, extending Mardia's Kurtosis test. In the continuity of this work, we provide here an original performance study of the latter test applied to two-dimensional projections. By leveraging copula, we conduct a comparative study between the bivariate tests and their scalar counterparts. This simulation study reveals that one-dimensional random projections lead to notably less powerful tests than two-dimensional ones.

A Random Matrix Perspective on Random Tensors

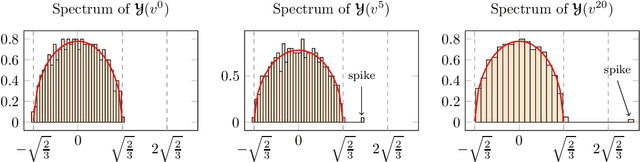
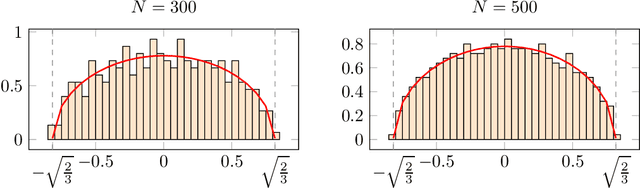
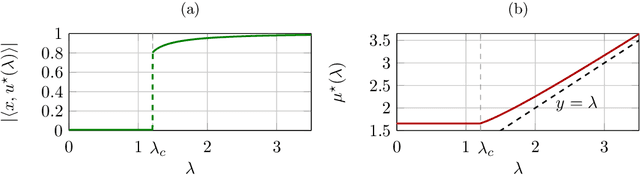
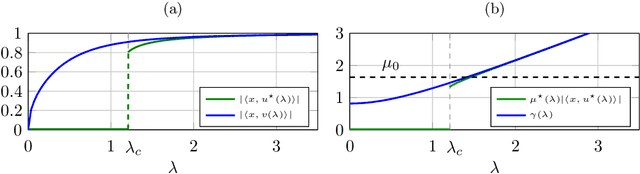
Tensor models play an increasingly prominent role in many fields, notably in machine learning. In several applications of such models, such as community detection, topic modeling and Gaussian mixture learning, one must estimate a low-rank signal from a noisy tensor. Hence, understanding the fundamental limits and the attainable performance of estimators of that signal inevitably calls for the study of random tensors. Substantial progress has been achieved on this subject thanks to recent efforts, under the assumption that the tensor dimensions grow large. Yet, some of the most significant among these results--in particular, a precise characterization of the abrupt phase transition (in terms of signal-to-noise ratio) that governs the performance of the maximum likelihood (ML) estimator of a symmetric rank-one model with Gaussian noise--were derived on the basis of statistical physics ideas, which are not easily accessible to non-experts. In this work, we develop a sharply distinct approach, relying instead on standard but powerful tools brought by years of advances in random matrix theory. The key idea is to study the spectra of random matrices arising from contractions of a given random tensor. We show how this gives access to spectral properties of the random tensor itself. In the specific case of a symmetric rank-one model with Gaussian noise, our technique yields a hitherto unknown characterization of the local maximum of the ML problem that is global above the phase transition threshold. This characterization is in terms of a fixed-point equation satisfied by a formula that had only been previously obtained via statistical physics methods. Moreover, our analysis sheds light on certain properties of the landscape of the ML problem in the large-dimensional setting. Our approach is versatile and can be extended to other models, such as asymmetric, non-Gaussian and higher-order ones.

Identifiability of an X-rank decomposition of polynomial maps

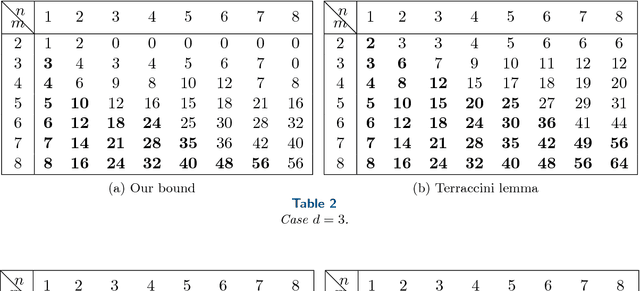
In this paper, we study a polynomial decomposition model that arises in problems of system identification, signal processing and machine learning. We show that this decomposition is a special case of the X-rank decomposition --- a powerful novel concept in algebraic geometry that generalizes the tensor CP decomposition. We prove new results on generic/maximal rank and on identifiability of a particular polynomial decomposition model. In the paper, we try to make results and basic tools accessible for general audience (assuming no knowledge of algebraic geometry or its prerequisites).

Robust Independent Component Analysis by Iterative Maximization of the Kurtosis Contrast with Algebraic Optimal Step Size

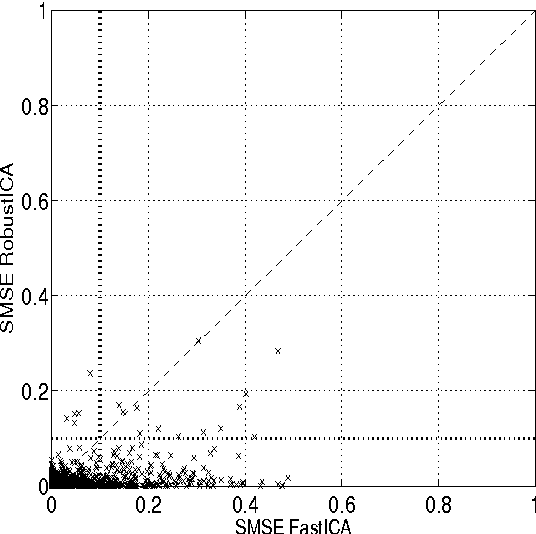
Independent component analysis (ICA) aims at decomposing an observed random vector into statistically independent variables. Deflation-based implementations, such as the popular one-unit FastICA algorithm and its variants, extract the independent components one after another. A novel method for deflationary ICA, referred to as RobustICA, is put forward in this paper. This simple technique consists of performing exact line search optimization of the kurtosis contrast function. The step size leading to the global maximum of the contrast along the search direction is found among the roots of a fourth-degree polynomial. This polynomial rooting can be performed algebraically, and thus at low cost, at each iteration. Among other practical benefits, RobustICA can avoid prewhitening and deals with real- and complex-valued mixtures of possibly noncircular sources alike. The absence of prewhitening improves asymptotic performance. The algorithm is robust to local extrema and shows a very high convergence speed in terms of the computational cost required to reach a given source extraction quality, particularly for short data records. These features are demonstrated by a comparative numerical analysis on synthetic data. RobustICA's capabilities in processing real-world data involving noncircular complex strongly super-Gaussian sources are illustrated by the biomedical problem of atrial activity (AA) extraction in atrial fibrillation (AF) electrocardiograms (ECGs), where it outperforms an alternative ICA-based technique.

Initialization Free Graph Based Clustering

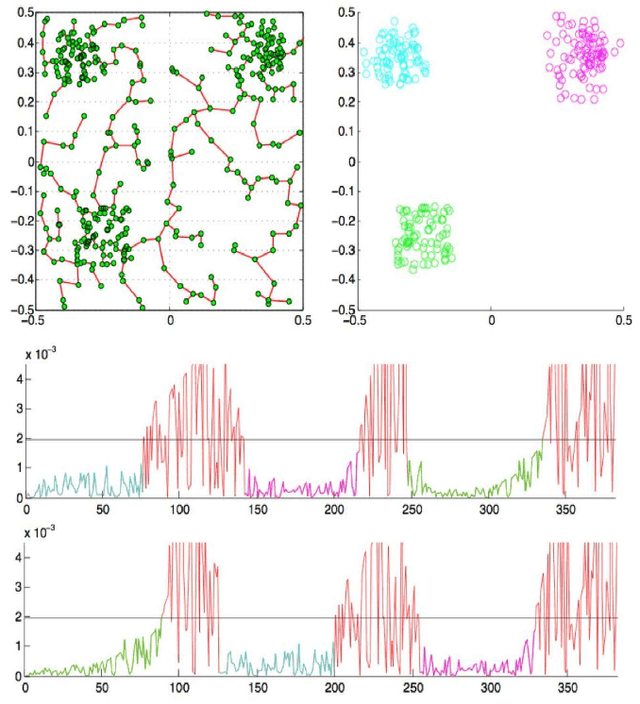
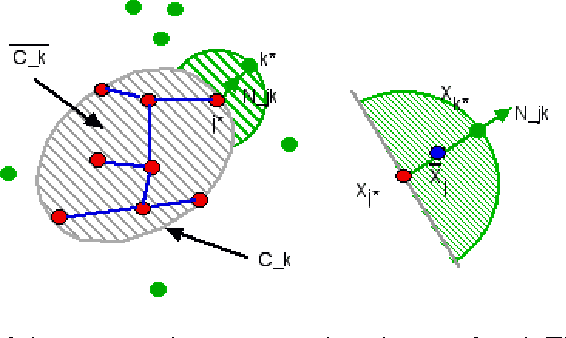
This paper proposes an original approach to cluster multi-component data sets, including an estimation of the number of clusters. From the construction of a minimal spanning tree with Prim's algorithm, and the assumption that the vertices are approximately distributed according to a Poisson distribution, the number of clusters is estimated by thresholding the Prim's trajectory. The corresponding cluster centroids are then computed in order to initialize the generalized Lloyd's algorithm, also known as $K$-means, which allows to circumvent initialization problems. Some results are derived for evaluating the false positive rate of our cluster detection algorithm, with the help of approximations relevant in Euclidean spaces. Metrics used for measuring similarity between multi-dimensional data points are based on symmetrical divergences. The use of these informational divergences together with the proposed method leads to better results, compared to other clustering methods for the problem of astrophysical data processing. Some applications of this method in the multi/hyper-spectral imagery domain to a satellite view of Paris and to an image of the Mars planet are also presented. In order to demonstrate the usefulness of divergences in our problem, the method with informational divergence as similarity measure is compared with the same method using classical metrics. In the astrophysics application, we also compare the method with the spectral clustering algorithms.